りお【2020センターⅡB大門1】三角関数
@hayato0121
三角関数の合成
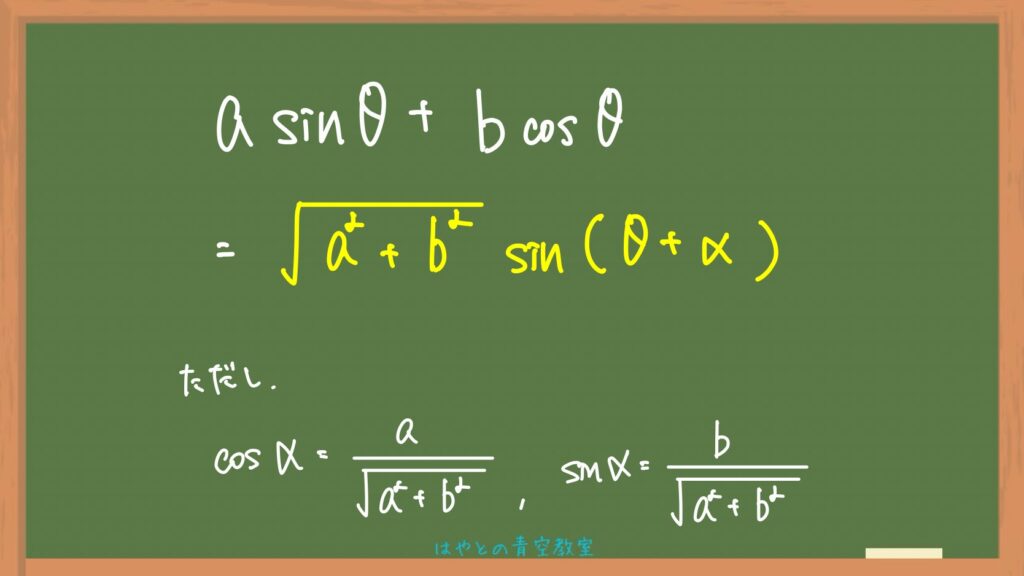
とりあえず、合成の公式はこれね!
教科書とかでも同じように書いてあると思うけど。
これのとうりやったら、わからんって言ってたとこ出ると思うぞ!
けど式で覚えるよりも図で覚えた方が簡単だと思うからちょっと解説入れとくね〜⬇️
復習:三角関数の合成
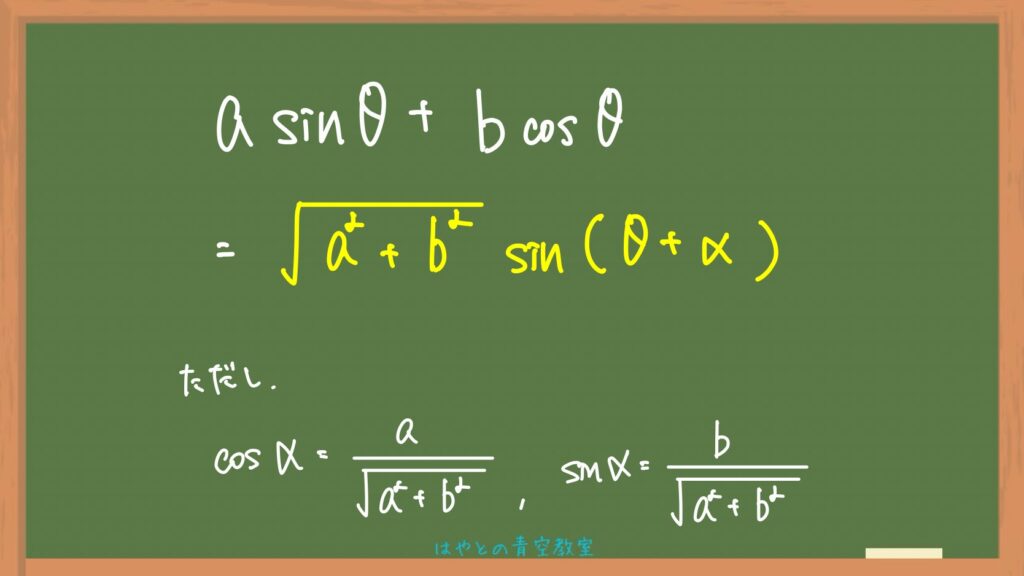
式で書いたのがこれなんだけど、図にするときは
sinの係数だけ横に、cosの係数だけ縦に線を引っ張って直角三角形をかく!
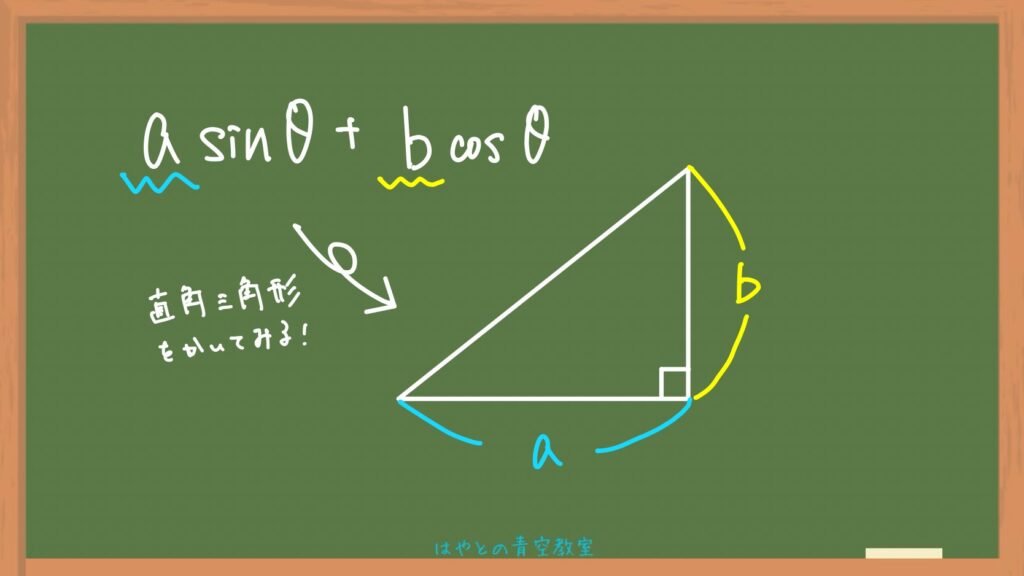
aとかbとかより数字の方が簡単と思うから例題でやるけど
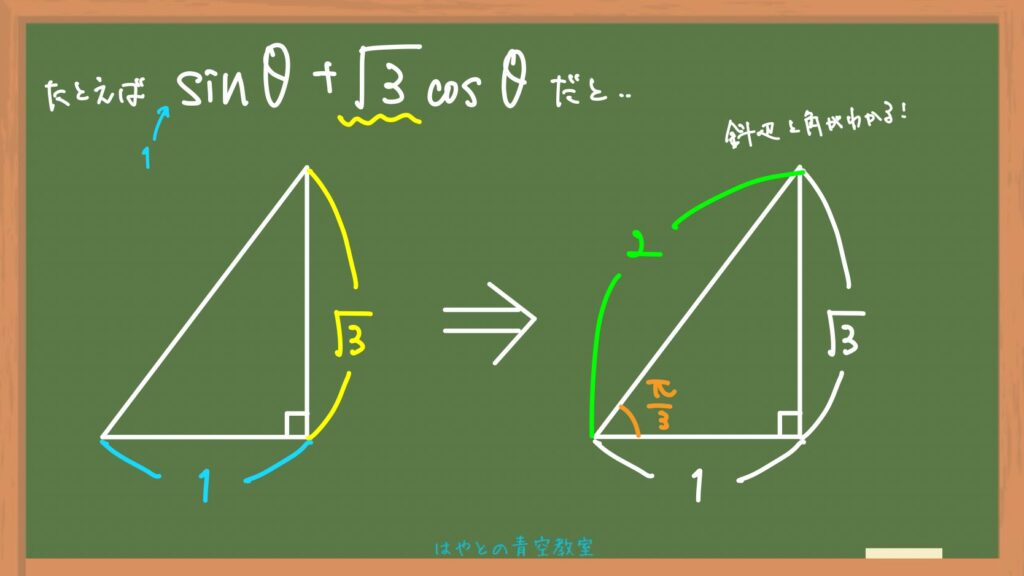
そしたら斜辺と角がわかるわけよ!
だいたい数字が出るように問題はなってると思うからそれを出して
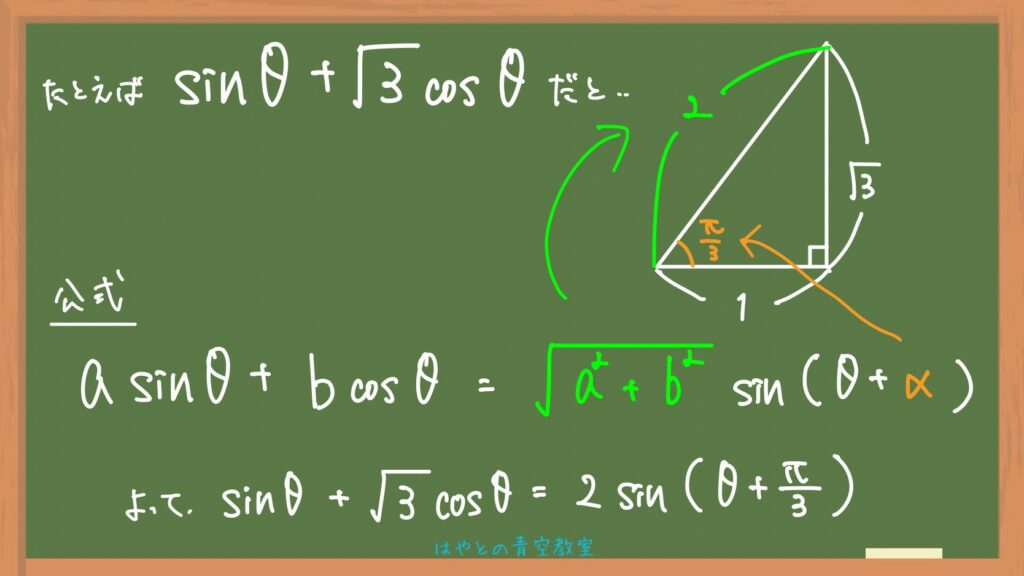
当てはめてみたら終わり〜!
ok?
(エ)を出す時は係数の2は両辺割られてないんかな!
問題解説
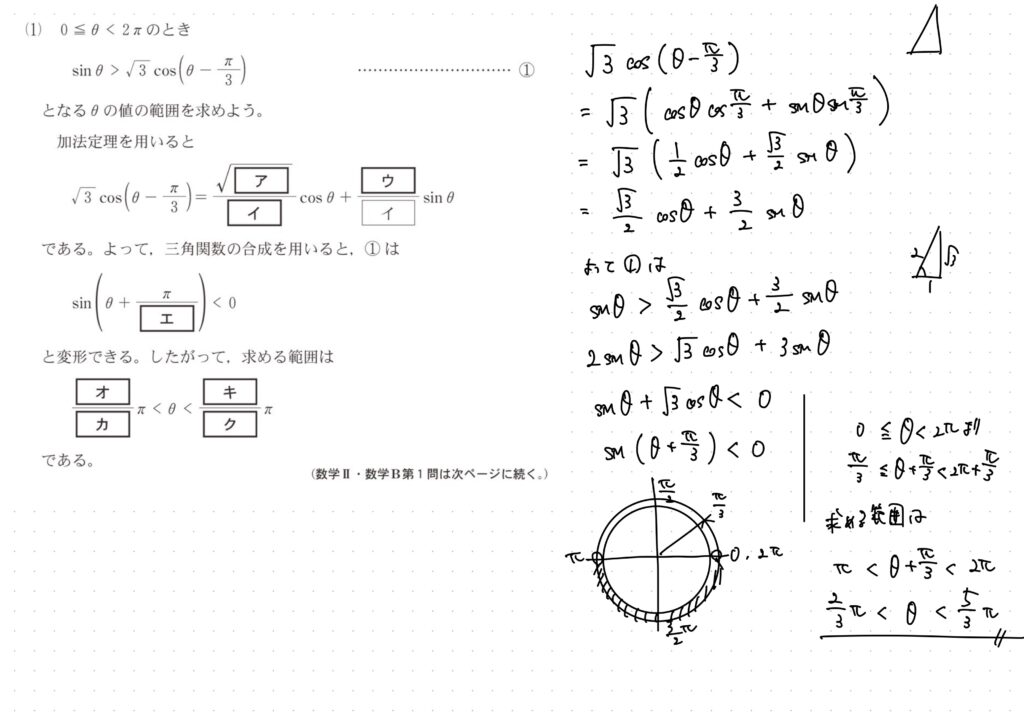
多分、模範解答も似たようなこと書いてて意味がわからんのよね?
ななみから聞いたところやと、範囲のところがわからんらしいから、
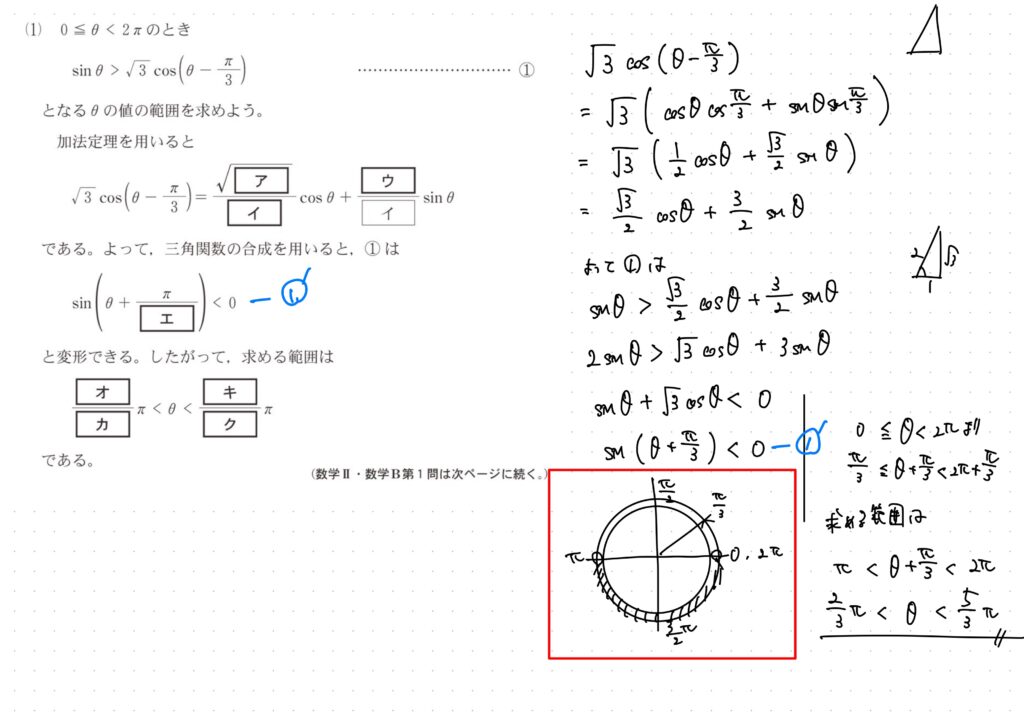
①’は出せたと思って進めるね
そこから進めるためには赤で囲った図を理解してくれたらいいんじゃないかとおもうんだけど、
この図が①’の式を図にしてて、
θの範囲はもともと0から2πまでなんだけど、①’の中のsinの中身が(θ+π/3)だから、これに合わせて今回はπ/3から2π+π/3までで考えますよってことになるわけよ。
それでπ/3のところで線引いてるわけね
だからπ/3をスタートして1周が、今回の範囲。
で、このπ/3から2π+π/3の範囲の中でsinが0より小さい範囲はどこですかっていうのを求めるわけで、それがπから2πやね。
これはわかるか?
よって、θ+π/3がπから2πが求める範囲ってことになって、式を整理すると答えが出てくる!
って、文にするとなんか難しいような気もしたけど伝わるかね?
わからんかったらまたどこわからんかったか教えてー!
