【解の公式の証明】現役数学講師がわかりやすく解説！
@hayato0121
はやとの青空教室
【三角比の相互関係】証明もわかりやすく現役数学講師が解説！
@hayato0121
記事内に商品プロモーションを含む場合があります
こんにちは！はやとです！
今回は、三角比の相互関係について解説します！
サイン、コサイン、タンジェントを上手に活用できるようになるための基礎として必ず覚えておきたい次の3つ⬇️
三角比の相互関係
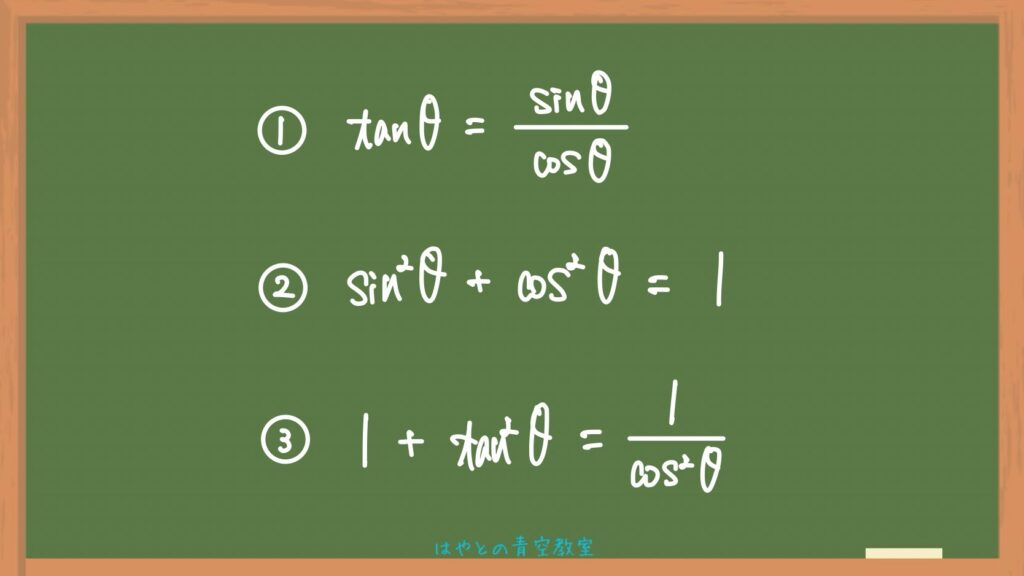
それぞれ、証明して導くこともできるんです⬇️
- ①の証明
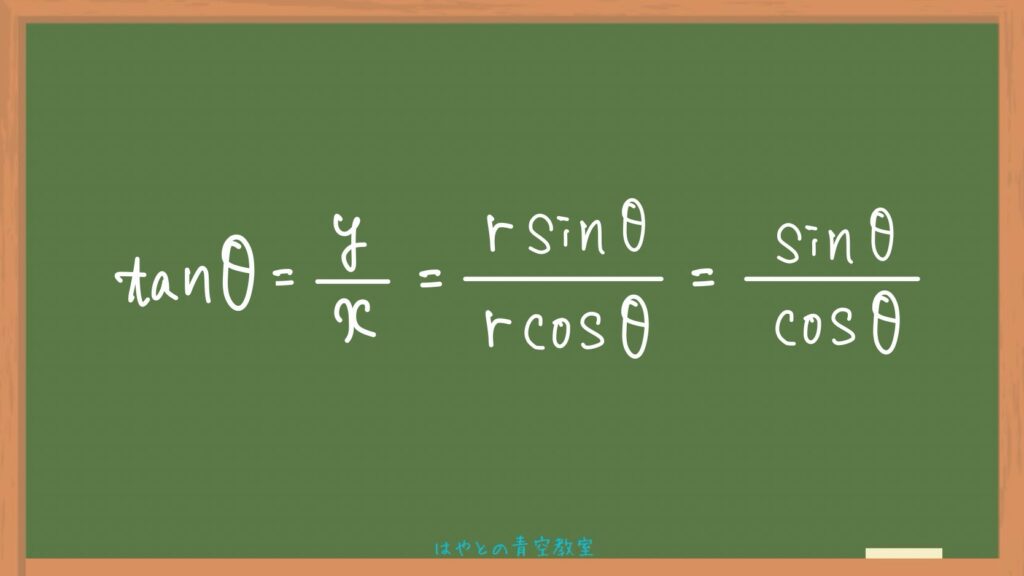
- ②の証明
- ③の証明
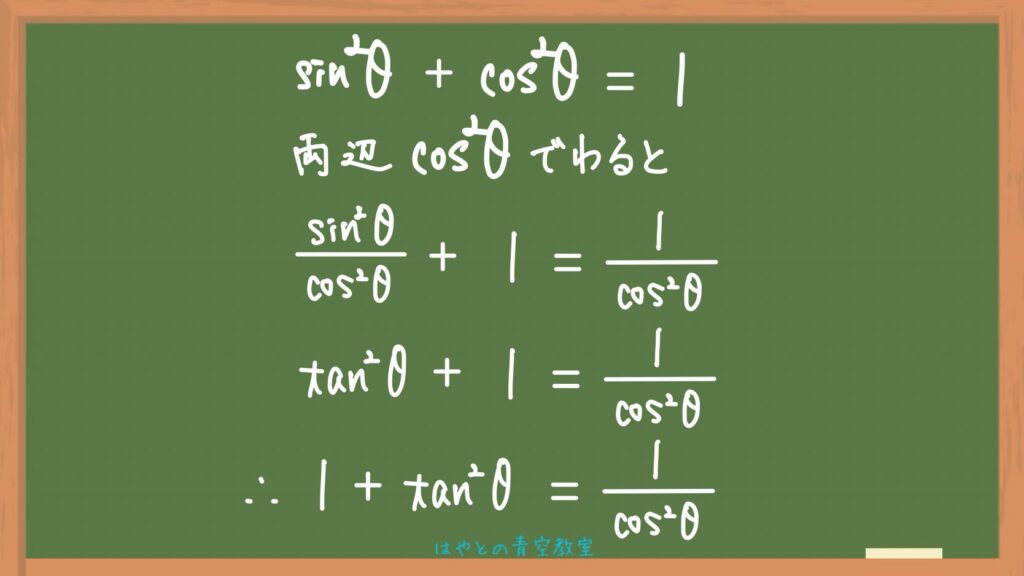
この記事では、詳しく証明の解説をしていきます！
黒板画像を長押しして保存！
待ち受けにして復習もオススメ👍
『はやとの青空教室』では数学の苦手克服にオススメな塾の紹介もしています！
【数強塾の口コミ・評判は？】現役数学講師が徹底分析！
【坪田塾で数学は得意になれるのか？】口コミと特徴から現役数学講師が徹底分析！
【坪田塾オンライン校の口コミ】現役数学講師が徹底分析！
数学講師歴7年のぼくの視点で解説しています！
三角比の定義
三角比の相互関係を証明するためには、三角比の定義をおさえておく必要があります。
その三角比の定義がこちら⬇️
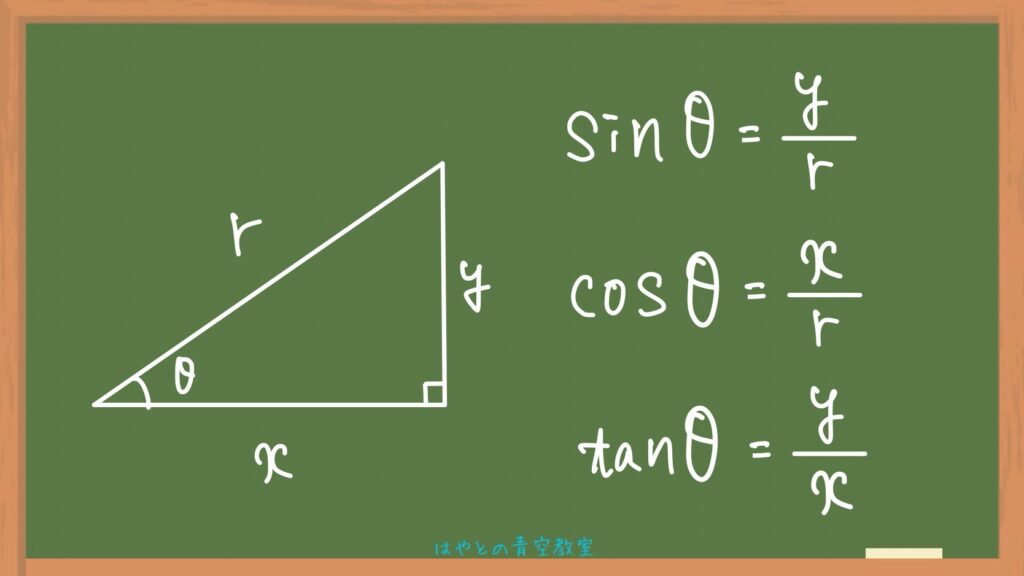
三角比は直角三角形における角と辺の長さから、定義されます。
定義はしっかり覚えておきましょう！
三角比の相互関係の証明
では、ここから三角比の相互関係について、証明の解説をしていきます！
改めて確認しておくと、今回証明していく三角比の相互関係の式は次の3つ⬇️
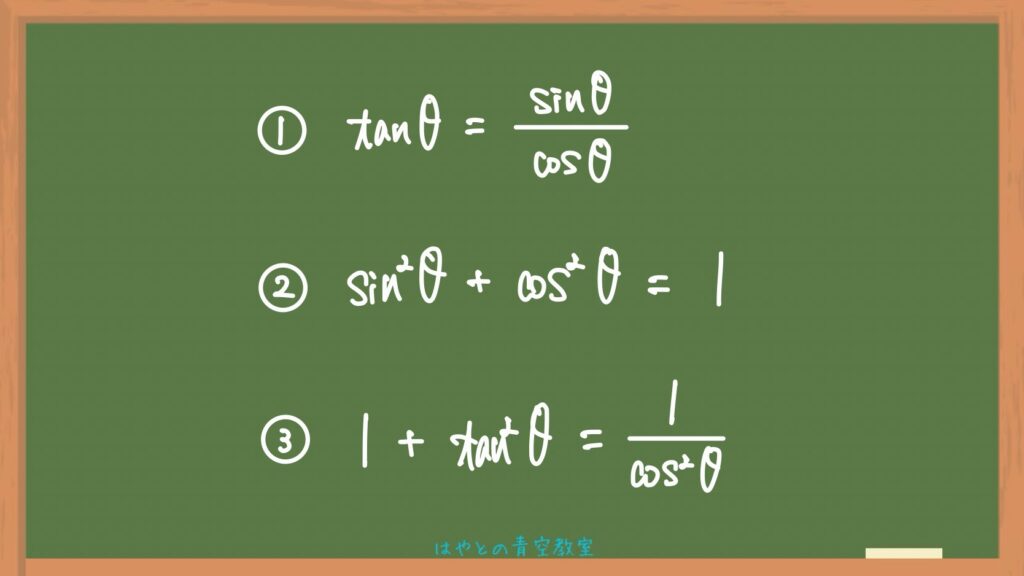
1つずつ解説していきます。
①の証明
まずはこの①の式から解説していきます。
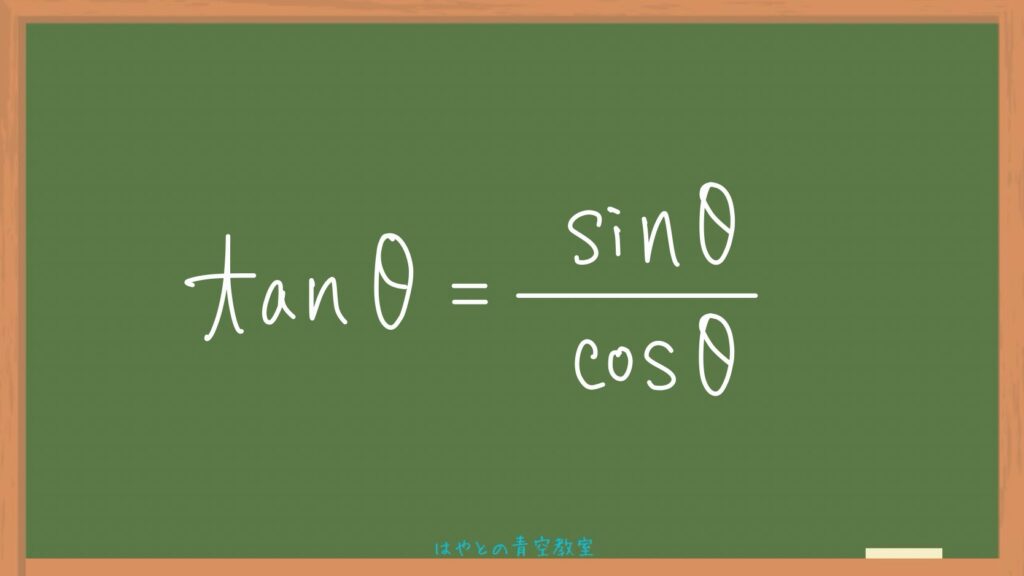
準備
証明するために、三角比の定義を活用します。
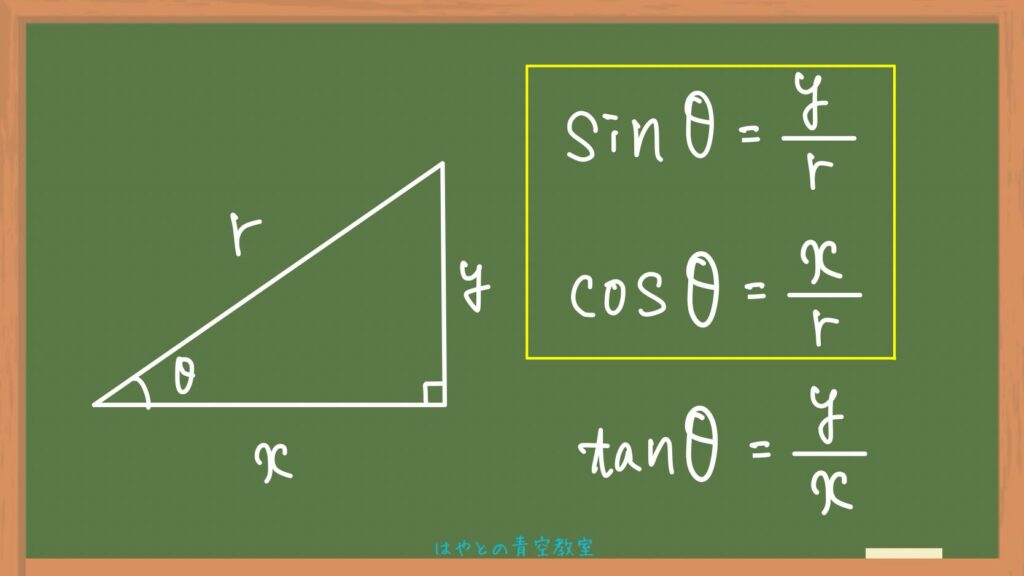
定義の中のsinとcosについて、両辺にrをかけて「x=」と「y=」の形をつくります。
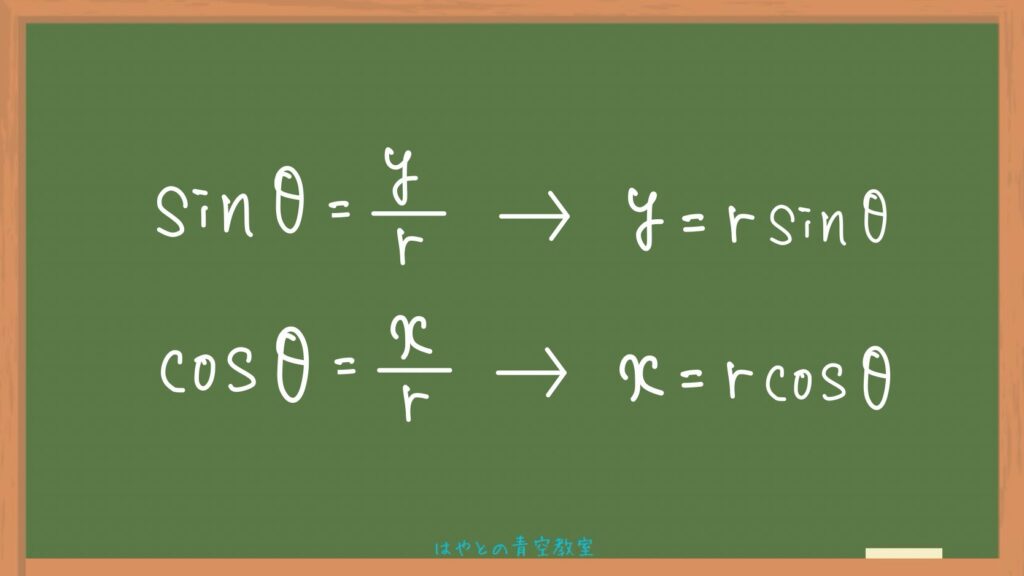
すると、こうなります。
代入
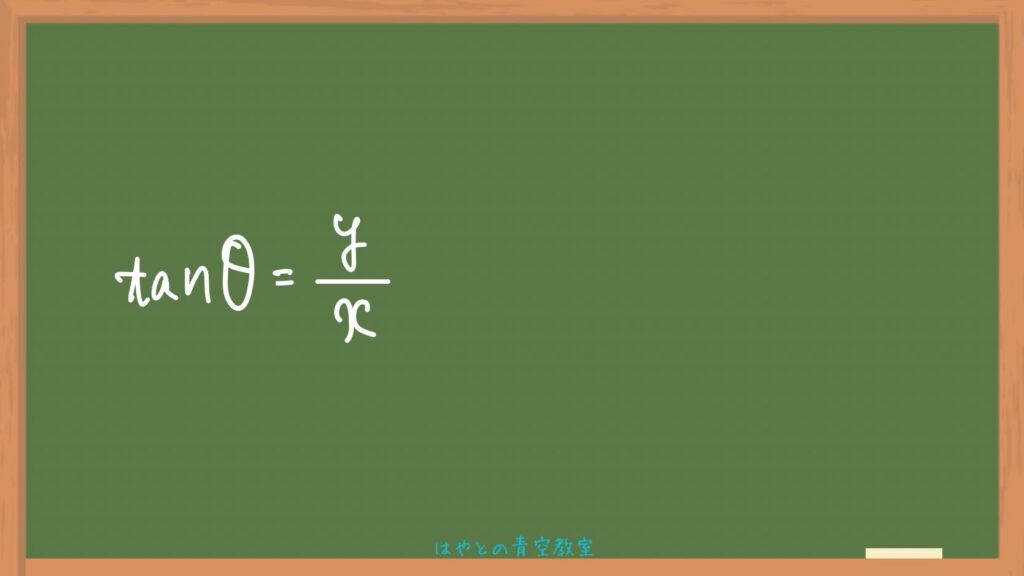
tanの定義はxとyで表されているので、そこに先ほど式変形した、「x=」「y=」の式の右辺を代入。
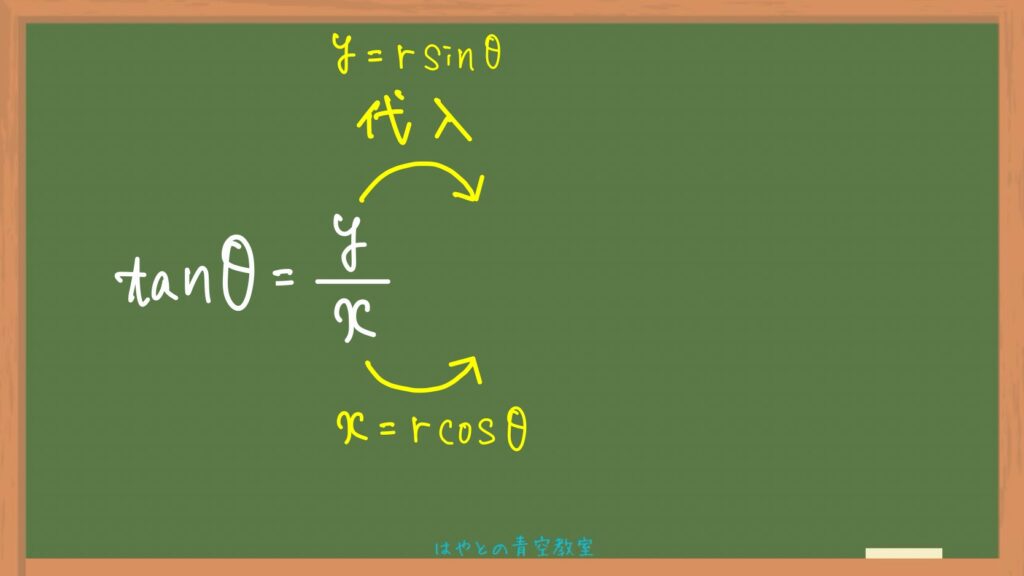
すると、こうなります⬇️
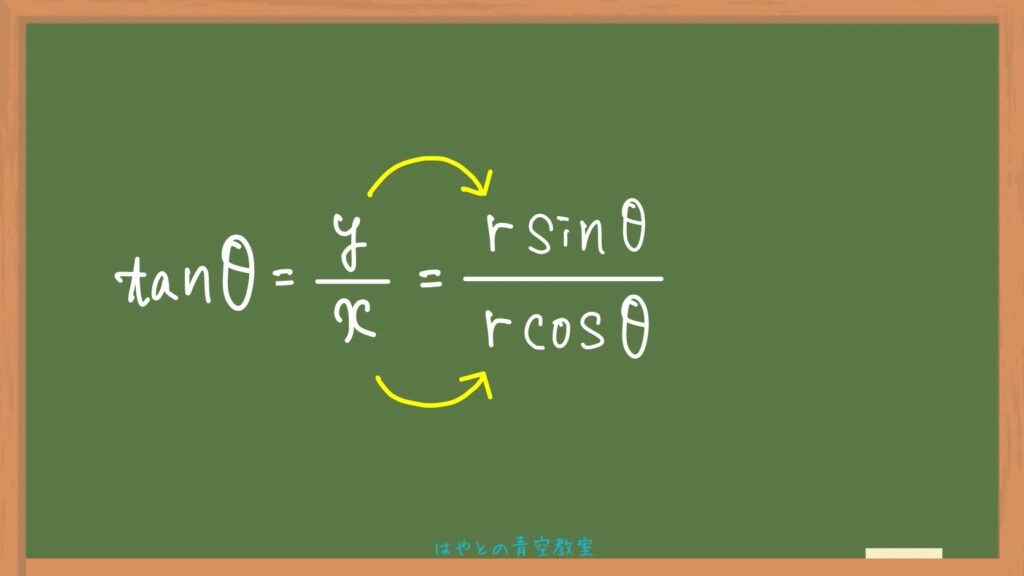
約分
代入した式の分子分母を見てみるとrで約分できるので約分をすると、
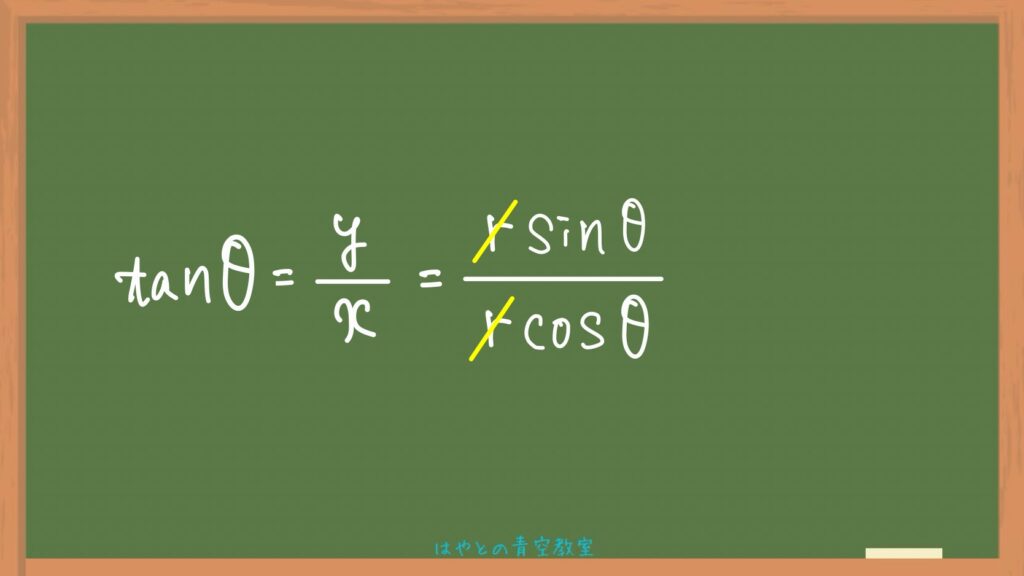
求める式の出来上がり👏
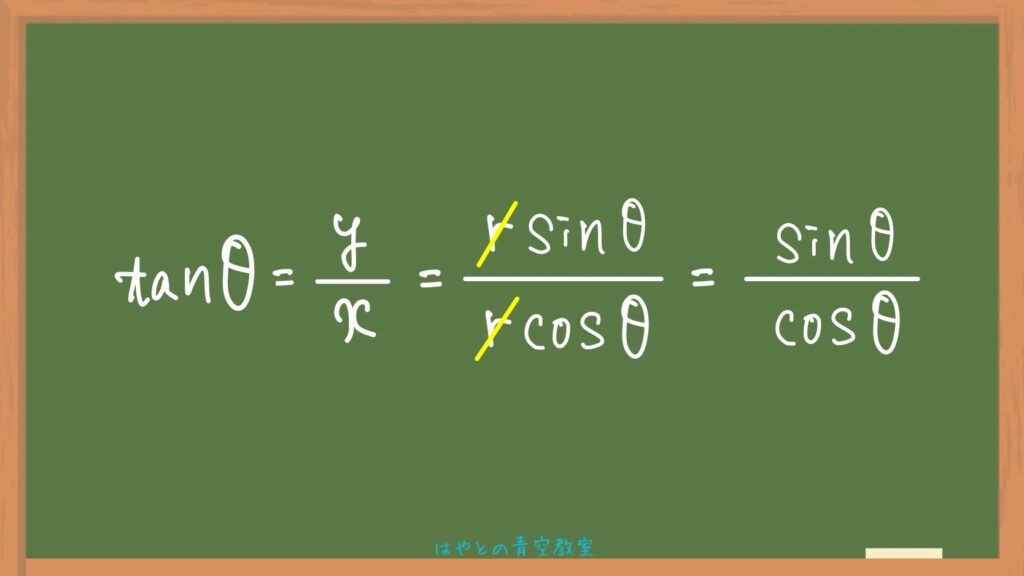
再度確認すると、三角比の相互関係1つ目の式はこの式ですね⬇️
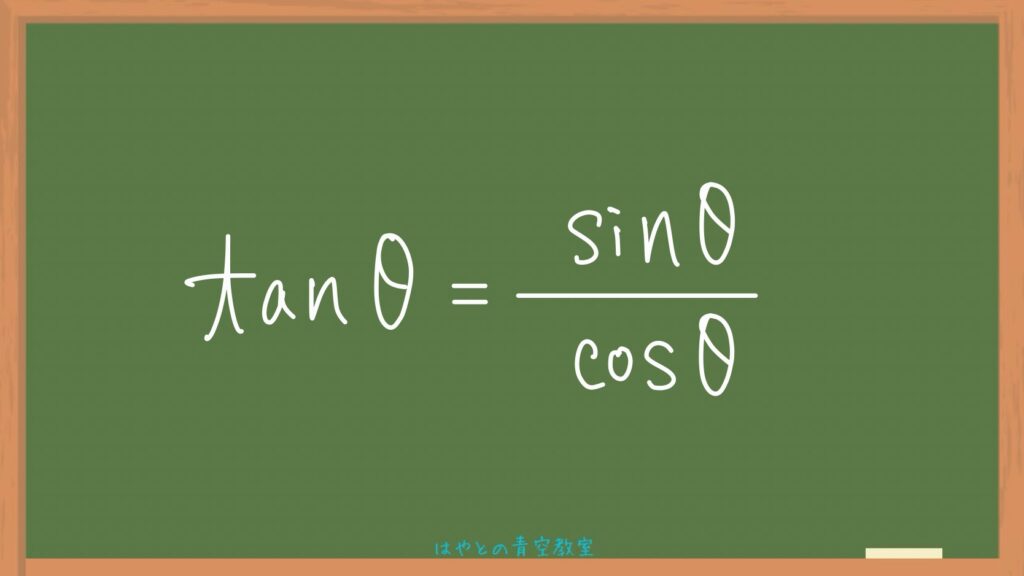
②の証明
次に、2つ目の証明にいきましょう！
証明するのはこの式⬇️
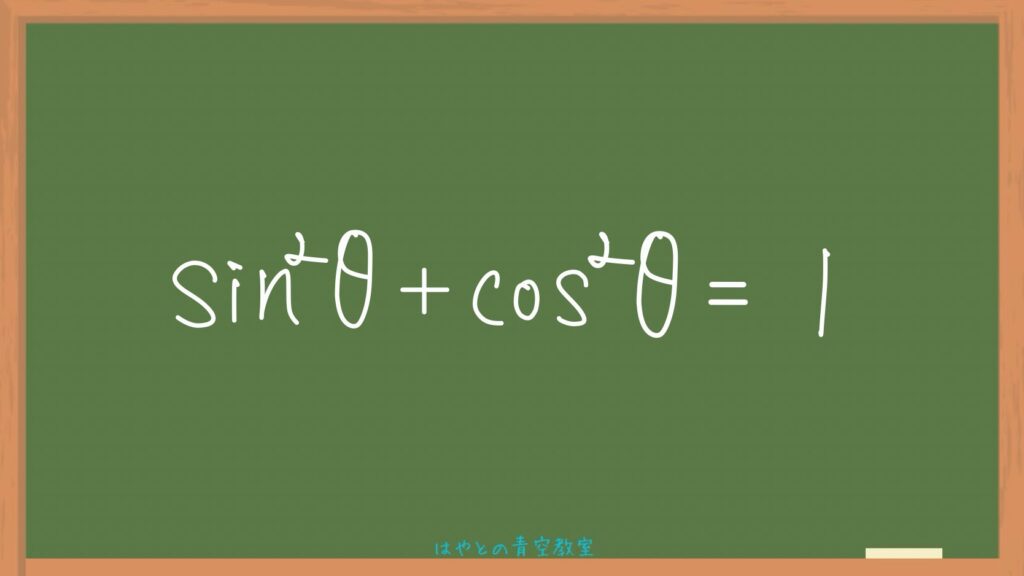
三平方の定理を利用
証明するために、三角比を定義する直角三角形について三平方の定理を使います。
すると、①式が出てきます。
代入
①式がx,y,rで表されているので、このxとyに三角比の定義を式変形して作った「x=」と「y=」の式の右辺を代入。
すると、
こうなるので展開をします。
両辺rの2乗で割る
展開すると両辺の各項にrの2乗が出てくるので、両辺rの2乗で割ります。
そうするとこうなるので⬇️
sinとcosの順番を入れ替えて
求める式の出来上がり👏
③の証明
最後に3つ目⬇️の証明です！
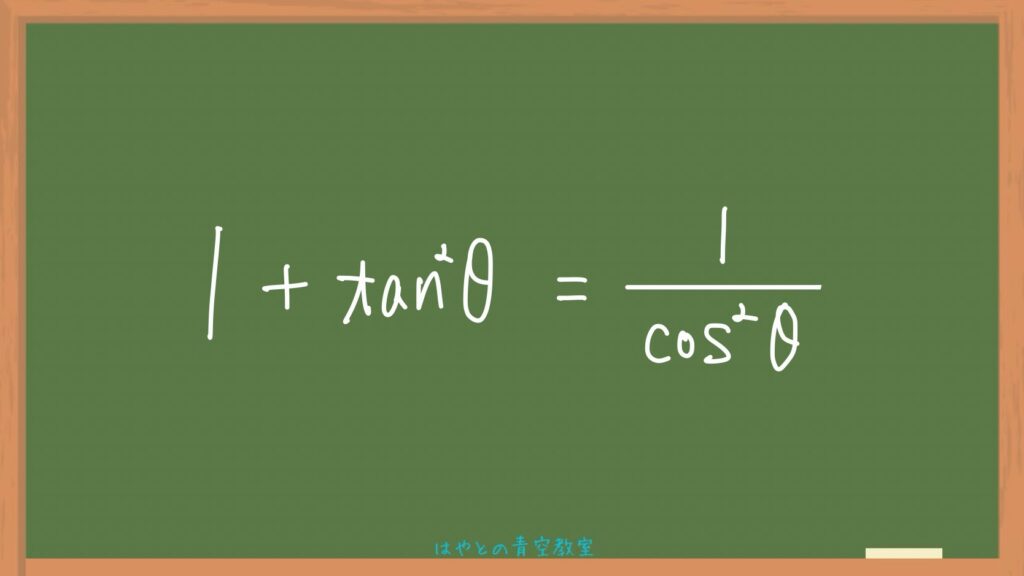
今回は三角比の相互関係②の式を使います。
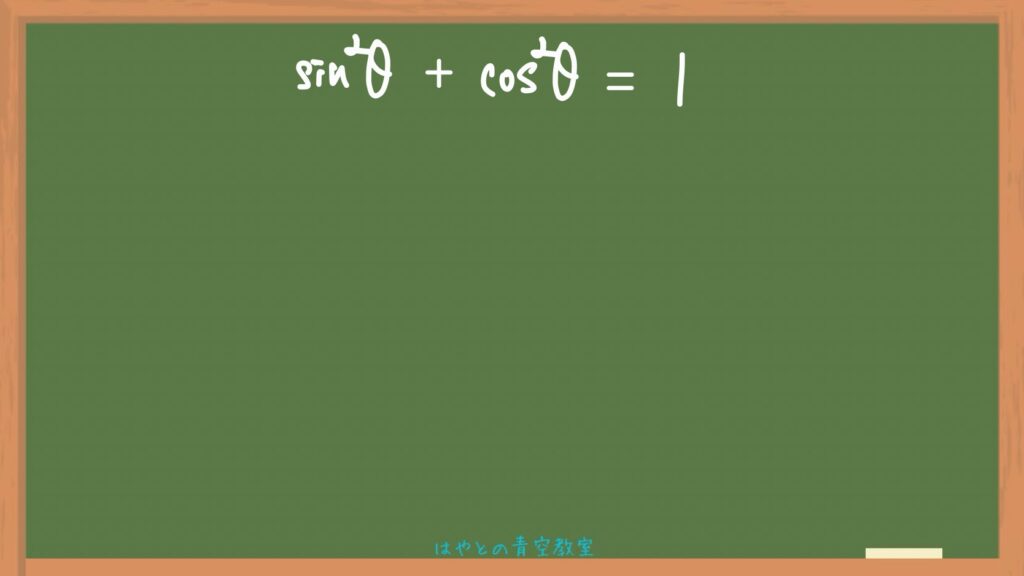
両辺cosの2乗でわる
まず、②の式をcosの2乗でわります。
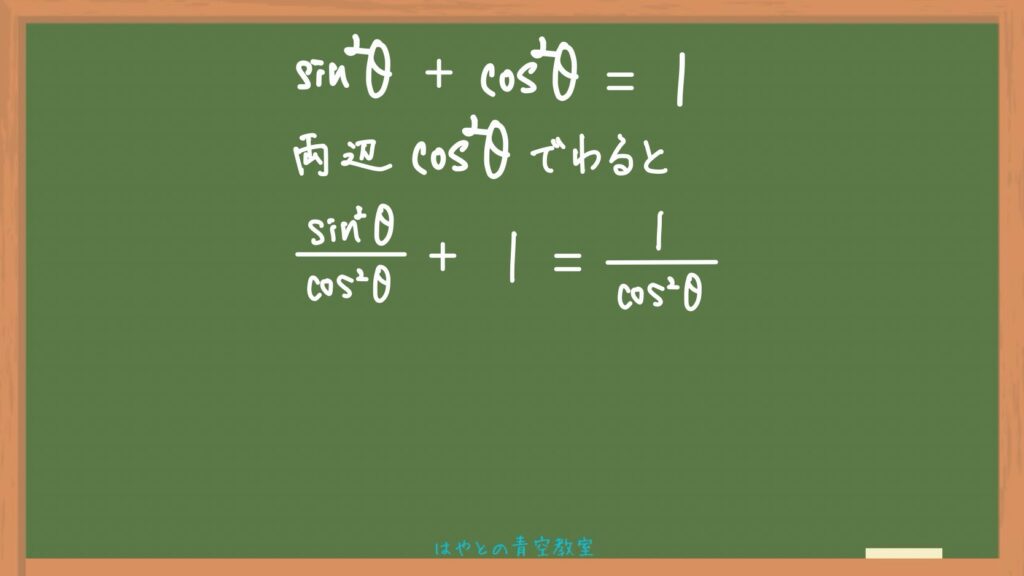
すると、tanに置き換えられる形が出てくるので置き換えます。
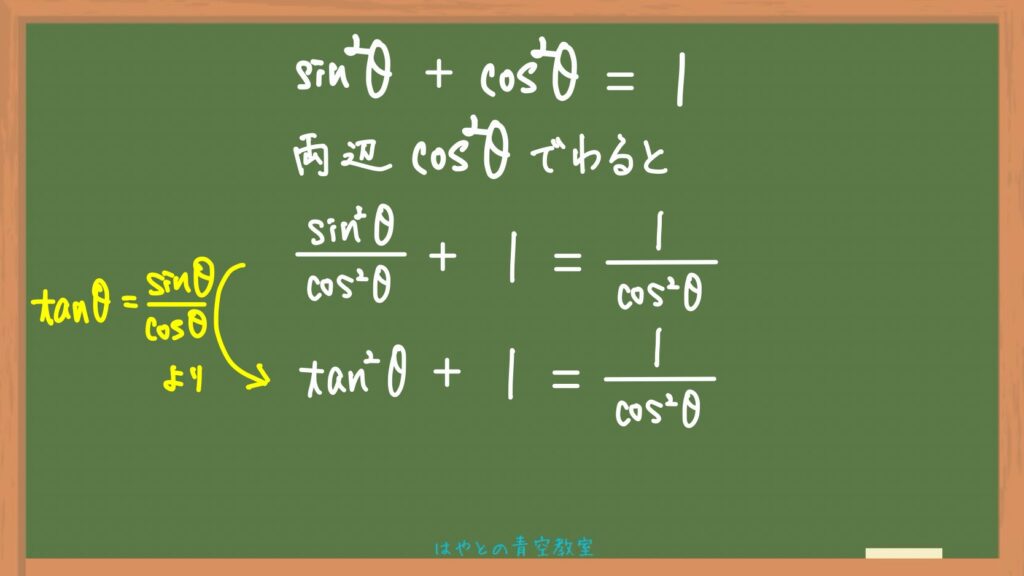
そしたら求める式の出来上がり👏
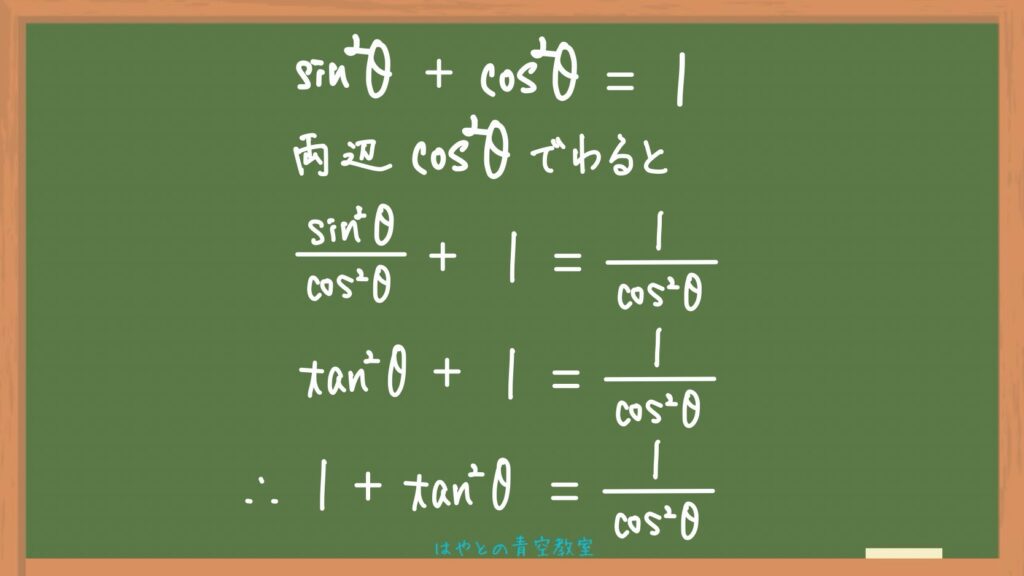
さいごに
今回は三角比の相互関係の式とその証明を紹介しました！
三角比の相互関係
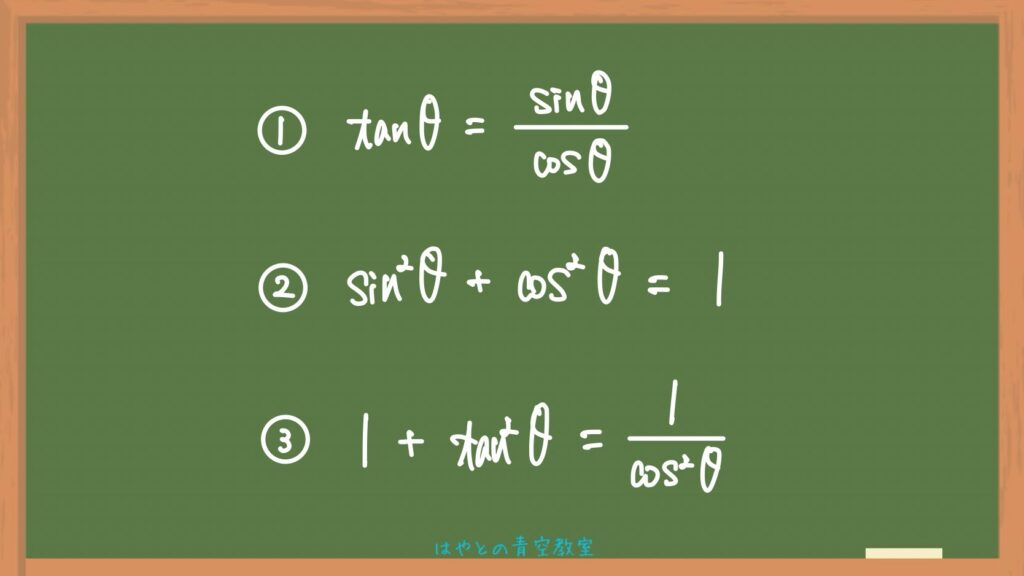
数Ⅱの三角関数でも使うことになる基礎なので、しっかりおさえておきましょう！
どうせやるなら楽しんで！
はやとの青空教室では、「数学がわかることで毎日の授業や数学の勉強が楽しくなったらいいな」という想いで数学の解説をしています！
確認したい公式が一目で見つかる、高校数学の公式をまとめた記事も公開しています⬇️
合わせて読みたい
【高校数学公式一覧】新課程に対応して現役数学講師が徹底解説！
また、数学の苦手克服、志望校合格にオススメな塾も紹介していますので、こちらもぜひ参考にしてみてください😌
オススメの塾を紹介！
【数強塾の口コミ・評判は？】現役数学講師が徹底分析！
【坪田塾で数学は得意になれるのか？】口コミと特徴から現役数学講師が徹底分析！
【坪田塾オンライン校の口コミ】現役数学講師が徹底分析！
塾選びに迷ったらこちらの記事がオススメです⬇️
合わせて読みたい
【塾選び】自分に合った授業形態の選び方のポイントを解説！
「このサイトが参考になった！」と思ったら是非お友達にも紹介してください！
数学や進路についての質問・相談がありましたら、お気軽に下のコメントから送ってください！お待ちしています！
ABOUT ME
7年目数学講師。中高数学非常勤講師／対面・オンライン家庭教師→公営塾スタッフ（地域おこし協力隊）▶︎数学の解説や塾選び、自身の体験談などについて記事にしています。
