【数学Ⅰ公式一覧】覚えておきたい公式を現役数学講師が徹底解説！
@hayato0121
はやとの青空教室
【工夫して解くたすき掛け】やり方を数学講師がわかりやすく解説！
@hayato0121
記事内に商品プロモーションを含む場合があります
こんにちは！はやとです！
今回は、工夫が必要なたすき掛けの問題について解説します！
やり方さえ理解できれば、次のような式の因数分解もできるようになります⬇️
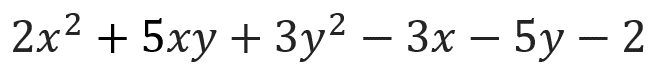
「簡単な因数分解なら分かったけど、文字や項が増えて複雑になるとわからなくなる」という人はぜひ、最後まで読んでみてください！
一緒に因数分解をマスターしていきましょう！
『はやとの青空教室』では数学の苦手克服にオススメな塾の紹介もしています！
【数強塾の口コミ・評判は？】現役数学講師が徹底分析！
【坪田塾で数学は得意になれるのか？】口コミと特徴から現役数学講師が徹底分析！
【坪田塾オンライン校の口コミ】現役数学講師が徹底分析！
数学講師歴7年のぼくの視点で解説しています！
応用問題に行く前に
早速応用問題！と行きたいところですが、基本を押さえていないとなかなか理解は進まないもの。
不安な人はこちらの記事で復習してから見てみてください⬇️
合わせて読みたい
【因数分解のやり方】公式〜たすき掛けまで現役数学講師が徹底解説！
この記事では、
- そもそも因数分解とは？
- 共通因数でくくる
- 公式の利用
- たすき掛け
これらについて実際に問題を紹介しながら解説しています。
応用編！
では今回の応用編、問題をみていきましょう！
置き換えを利用
問題
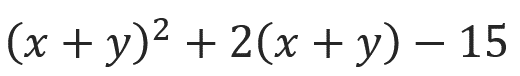
まずは、この問題について考えましょう。
今までは、x²+x+1のように、xなどという1つの文字についての2次式について考えてきました。
しかし今回は、xだった部分がx+yという形になってます。
そこで、x+yの部分をAと置き換えて考えてみましょう。
そうすると、元の式は
という形で表せます。
この式を因数分解すると、
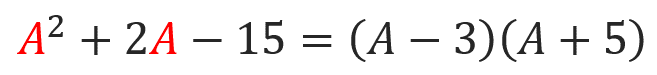
となる。
最後に、Aをx+yの形に戻せば、完了です。
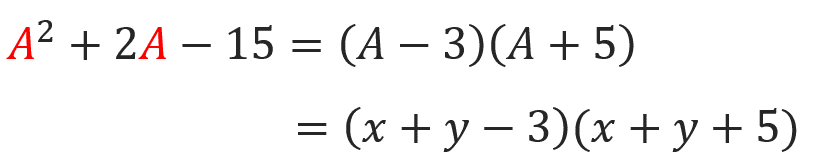
慣れてくると、置き換えをしなくてもx+yを1つのかたまりとしてみて、そのまま考えられるようになりますよ！
慣れるまでは、置き換えをしながら丁寧に計算を進めましょう。
最後に、置き換えずに解けた場合の回答例を紹介しておきます。
解答
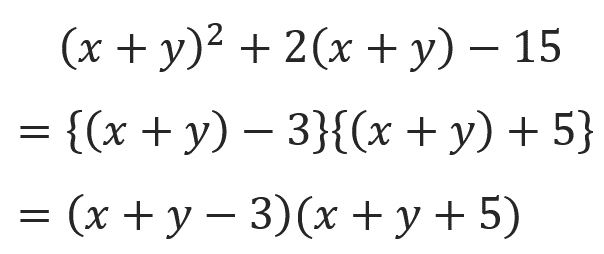
次数が低い文字で式を整理
では2問目。
問題
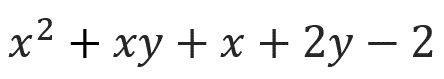
次はこんな問題です。今回も文字が2種類あるんだけど置き換えようがない。
こんな問題のときどうするかというと、次数が低い方の文字について式を整理していきます。
次数というのは文字の右上にある数字
いつも「～乗(じょう)」って呼んでるところです。
今回の問題の式では、xについて見てみると、x²の項があるので、xの次数は「2」となります。
（xの項もありますが、一番数字が大きいものがその式の次数となります。）
そして、yの次数は「1」
ということで、この問題の式では、yの方が次数が低いことになります。
yの方が次数が低いことがわかったので、今回は問題の式をyについて整理することになります。
yがついている項はまとめて、それ以外は外に、という感じです。
やってみると、
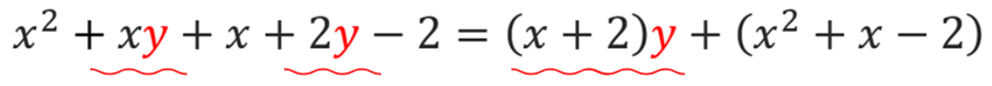
こうなります。
そしたら次に、x²+x-2の部分をいったん因数分解。
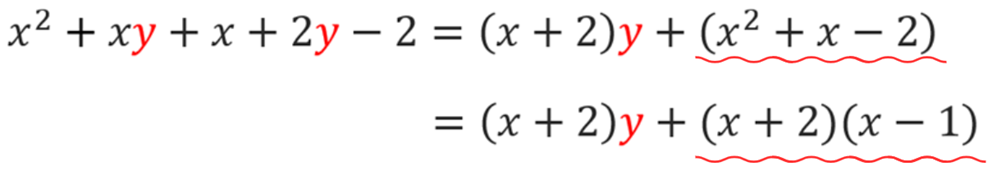
さぁ、この式⬆️をじ～～～っと見て、何か気づきませんか？？
そう、x+2が共通因数として出てきているんです！
なので、最後はx+2でくくったら完了！
ということで、ここまでの工程も含めて解答をまとめると、
解答
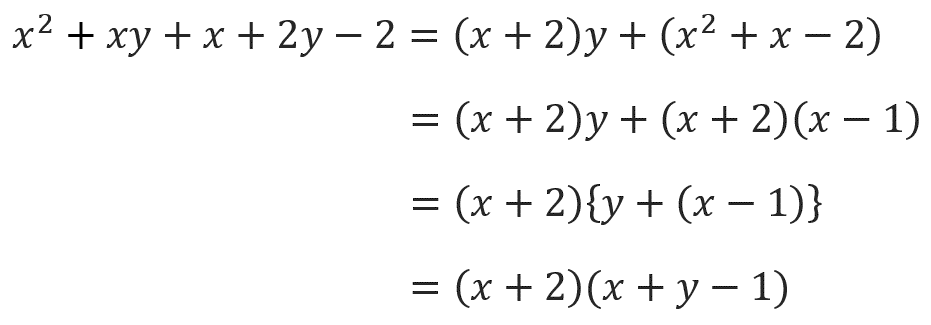
2種類の文字で次数が同じ（2次）場合
3問目。これで最後です。
問題
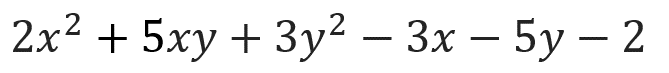
式、長いですね。そして、xもyも2次。
「んーー、どうしよーーー！」
って感じですが、こんなときどうするかというと、xとyの次数が同じなので、xかyどちらでもいいので降べきの順に整理してみる。
まずはこれをやりましょう。
ここからの解説ではxについて整理していきますね。
まず、xについて降べきの順に整理してみるとこうなります⬇️
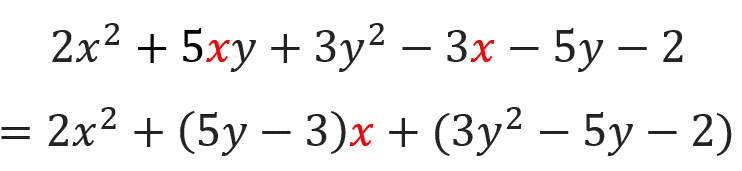
そしたら次に、3y²-5y-2の部分を因数分解していきましょう！
たすき掛けをして～
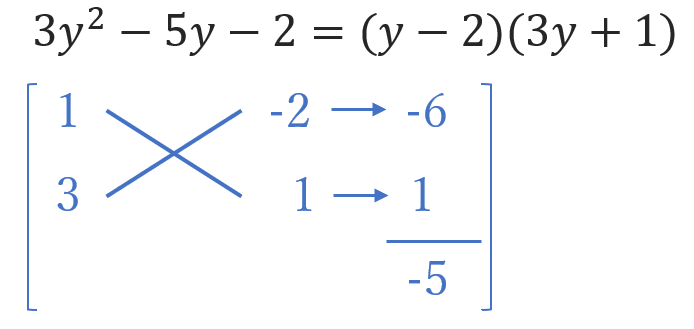
こうなるので、元の式に戻ると、
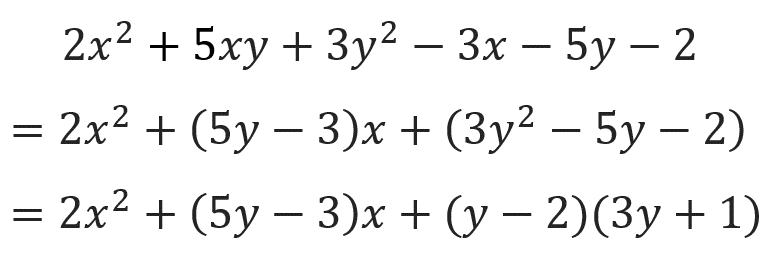
こんな感じ。
yについての2次式を因数分解したことで、掛け算の形をつくることができました！
これの何が良いかというと、
最後にこの問題の式全体を、xについての2次式とみて、
たすき掛けを利用し、因数分解して完了という流れになるんです！
やってみると、
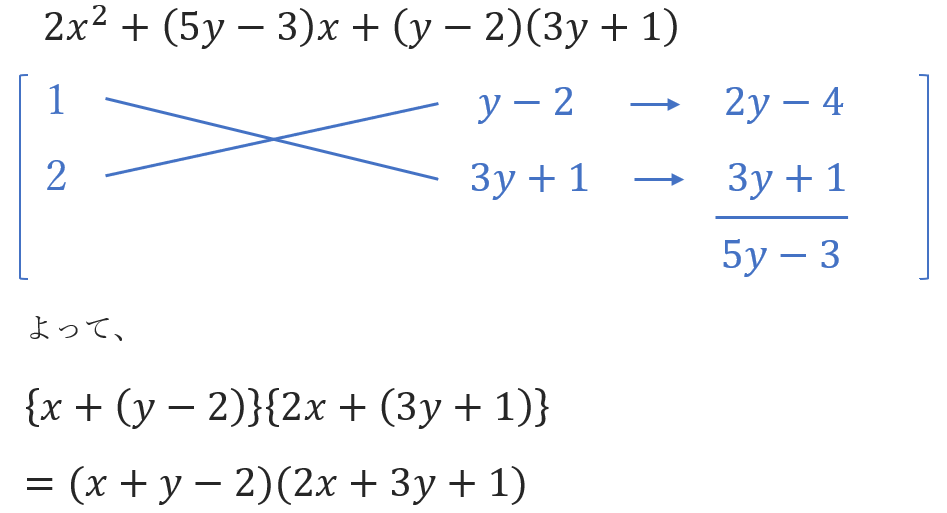
こうなります。
たすき掛けの部分が少し難しいかもしれませんが、やってることは基本のたすき掛けと同じ！
x²の係数になる掛け算の組み合わせと、定数項（今回はyの式）の部分になる掛け算の組み合わせでたすき掛けを考えます。
最後に解答をまとめたものを紹介しておきます⬇️
解答
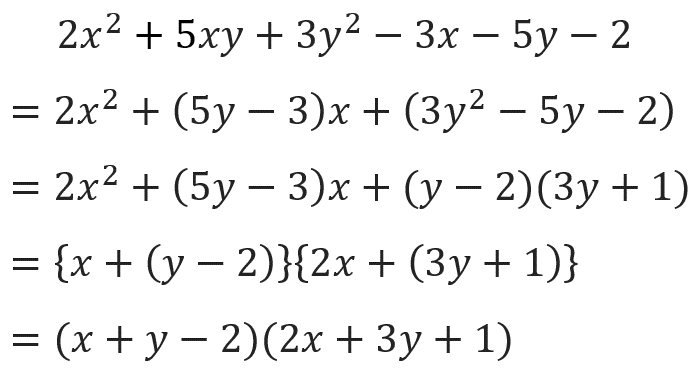
さいごに
今回は、工夫が必要なたすき掛けの問題について、解説してきました！
一見難しくは見えるかもしれませんが、やり方が分かれば必ずできるようになります！
工夫のポイント
- 置き換えを利用する
- 次数が低い方の文字で式を整理する
- 次数が同じであればどちらか自分で決めて整理する
どんどん手を動かして練習しましょう！
この記事で紹介した問題だけでなく、自分で持っている教科書や、テキストの問題でも練習を繰り返して、マスターしていってくださいね！
どうせやるなら楽しんで！
はやとの青空教室では、「数学がわかることで毎日の授業や数学の勉強が楽しくなったらいいな」という想いで数学の解説をしています！
確認したい公式が一目で見つかる、高校数学の公式をまとめた記事も公開しています⬇️
合わせて読みたい
【高校数学公式一覧】新課程に対応して現役数学講師が徹底解説！
数学の苦手克服、志望校合格にオススメな塾も紹介していますので、こちらもぜひ参考にしてみてください😌
オススメの塾を紹介！
【数強塾の口コミ・評判は？】現役数学講師が徹底分析！
【坪田塾で数学は得意になれるのか？】口コミと特徴から現役数学講師が徹底分析！
【坪田塾オンライン校の口コミ】現役数学講師が徹底分析！
塾選びに迷ったらこちらの記事がオススメです⬇️
合わせて読みたい
【塾選び】自分に合った授業形態の選び方のポイントを解説！
「このサイトが参考になった！」と思ったら是非お友達にも紹介してください！
数学や進路についての質問・相談がありましたら、お気軽に下のコメントから送ってください！お待ちしています！
ABOUT ME
7年目数学講師。中高数学非常勤講師／対面・オンライン家庭教師→公営塾スタッフ（地域おこし協力隊）▶︎数学の解説や塾選び、自身の体験談などについて記事にしています。
