【工夫して解くたすき掛け】やり方を数学講師がわかりやすく解説！
@hayato0121
はやとの青空教室
【数Ⅰ】三角比の公式（定理）一覧と証明。使い所も解説！
@hayato0121
記事内に商品プロモーションを含む場合があります
こんにちは！はやとです！
今回は三角比の公式一覧の紹介です。
数Ⅰ三角比の単元で覚えておきたい公式がこちら⬇️
この記事では、
- なぜこの公式(定理)が成り立つのか
- どんな時に使うのか
これらについて解説していきます。
『はやとの青空教室』では数学の苦手克服にオススメな塾の紹介もしています！
【数強塾の口コミ・評判は？】現役数学講師が徹底分析！
【坪田塾で数学は得意になれるのか？】口コミと特徴から現役数学講師が徹底分析！
【坪田塾オンライン校の口コミ】現役数学講師が徹底分析！
数学講師歴7年のぼくの視点で解説しています！
三角比の相互関係
まずは、三角比の相互関係についてです！
覚えたい式は次の3つ⬇️
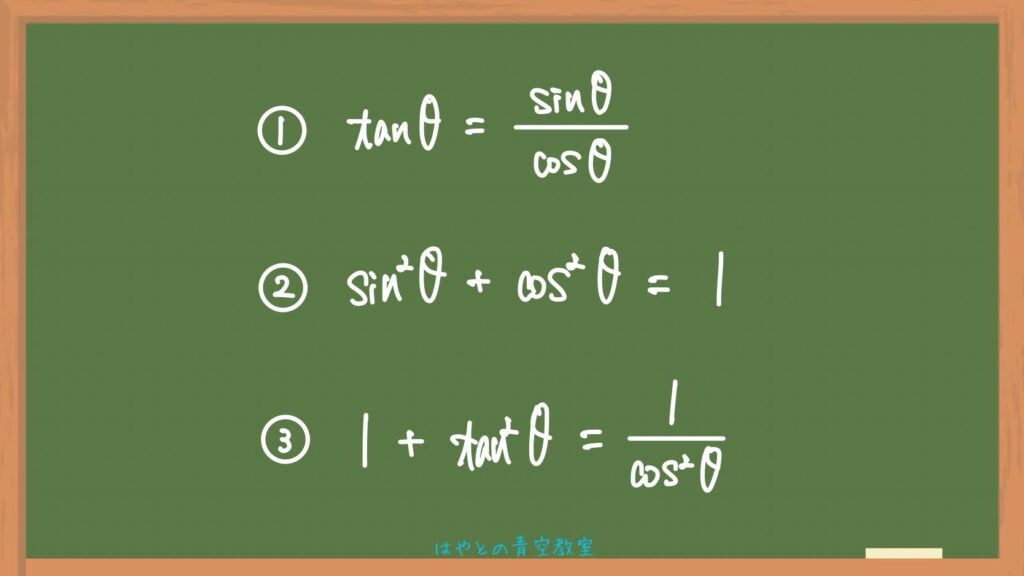
数Ⅰで習う三角比、数Ⅱで習う三角関数、さらにその先の微分積分などこの式はよく使うので覚えておきましょう！
証明
この3つの式は三角比の定義から、証明することができます。
証明の全体像を、ここでは紹介します。
①の証明
①の証明はこちら。
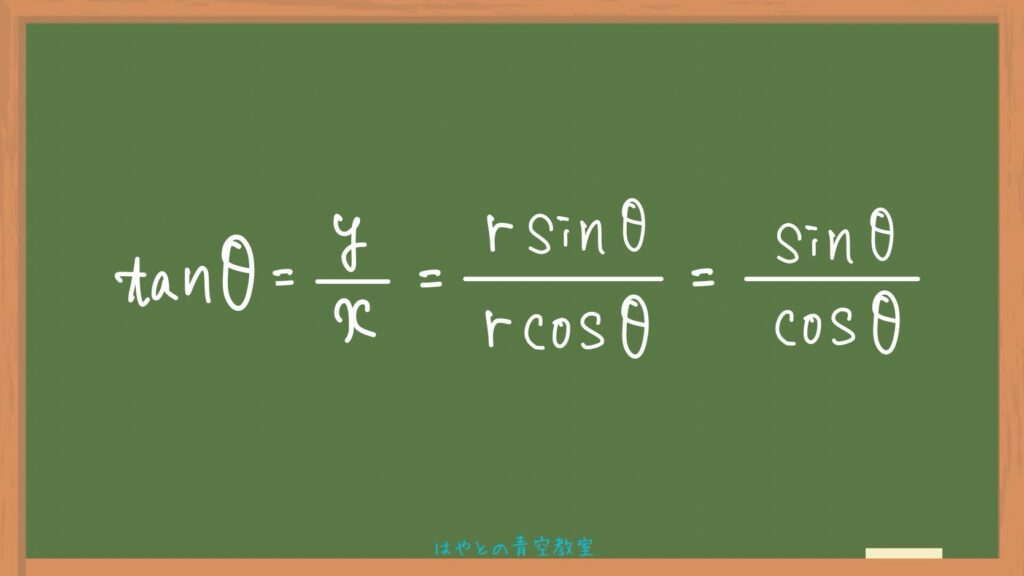
式変形を行うことで、導くことができます！
②の証明
②の証明がこちら。
最初の、三平方の定理を活用する部分が、ポイントですね！
③の証明
最後に、③の証明です。
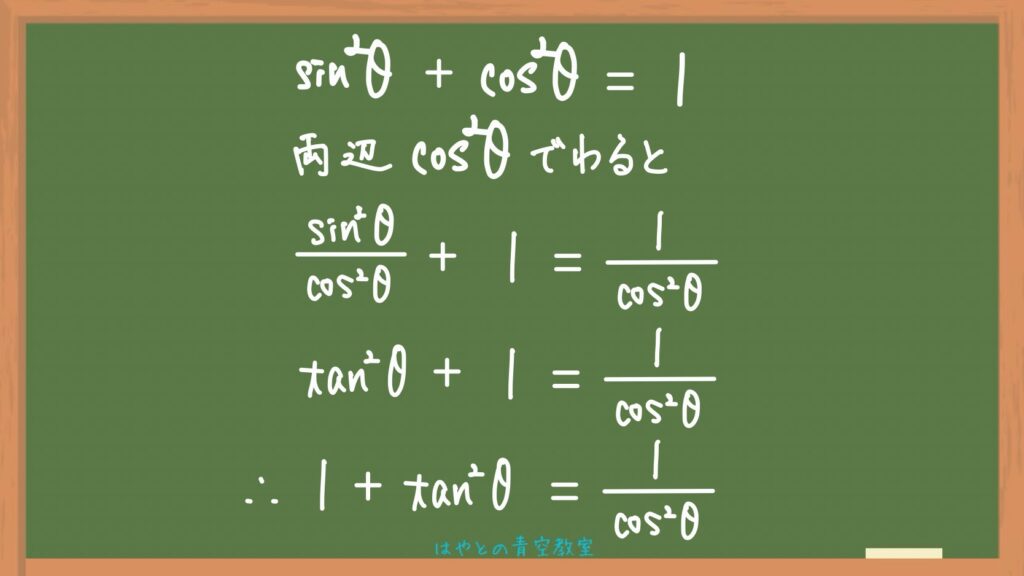
②の式を活用して、導くことができます。
さらに詳しい解説はこちら⬇️の記事で解説していますので、詳しく見たい方は是非読んでみてください！
合わせて読みたい
【三角比の相互関係】証明もわかりやすく現役数学講師が解説！
正弦定理
次に正弦定理の紹介です！
三角形の辺の長さとと角の大きさ、外接円の半径Rについて次の式が成り立ちます。
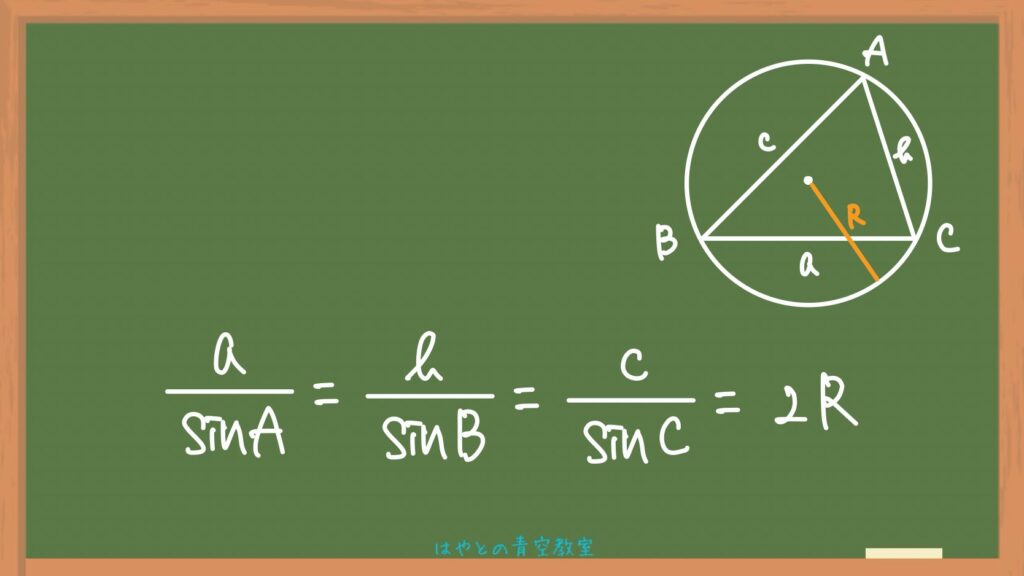
証明
正弦定理について、ここではAに着目した証明を紹介します。
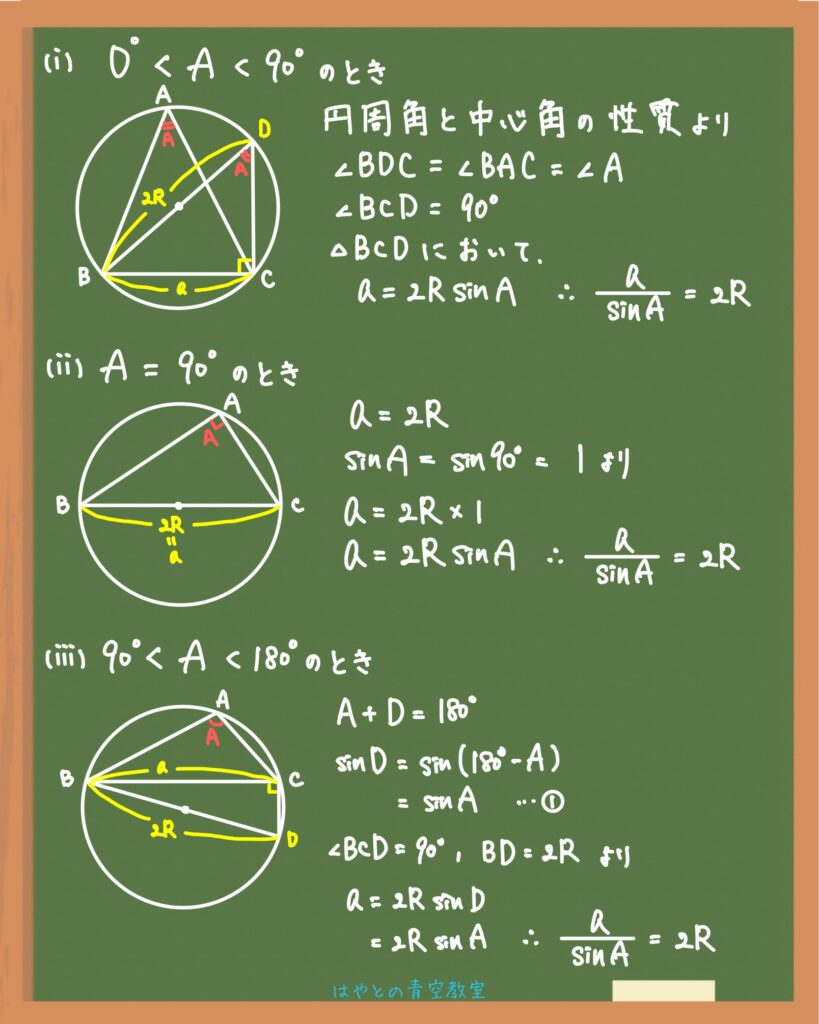
同様にして、BとCについても2Rと等しくなる式を導くことができるので、定理のように少し長い式ができあがります。
使い方
実際に正弦定理を活用して問題を解く時には、定理の式の1部分を使い、辺の長さや角、外接円の半径を求めます。
例題：辺の長さを求める
では、辺の長さを求める問題を1つ紹介します。
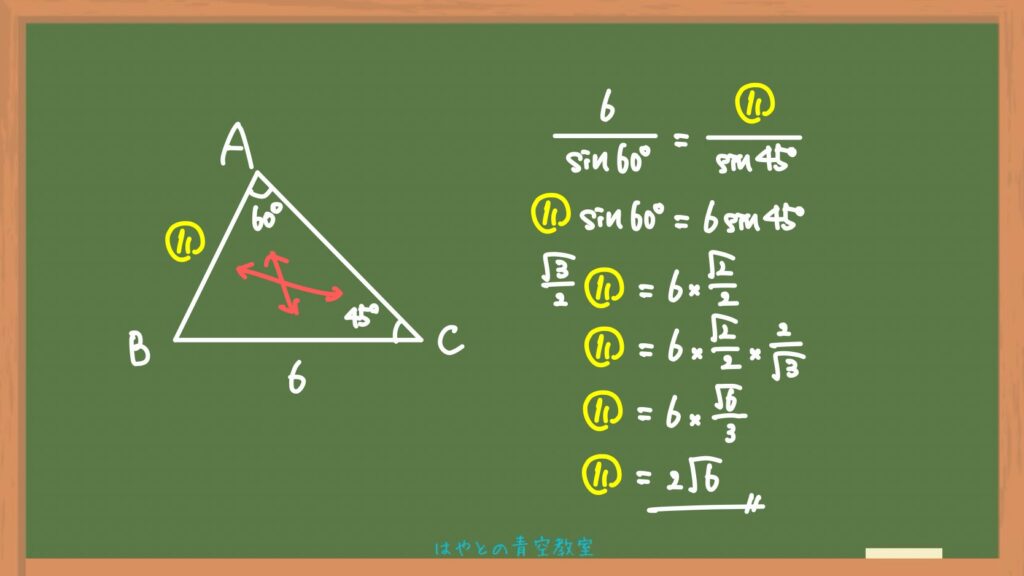
向かい合う1組の辺と角、そして求めたい辺とその向かい合う角について、正弦定理を活用しました。
正弦定理ではこのように、向かい合う辺と角について着目するのがポイントです！
余弦定理
次に、余弦定理の紹介です。
3辺の長さと1つの角から、次の式が成り立ちます。
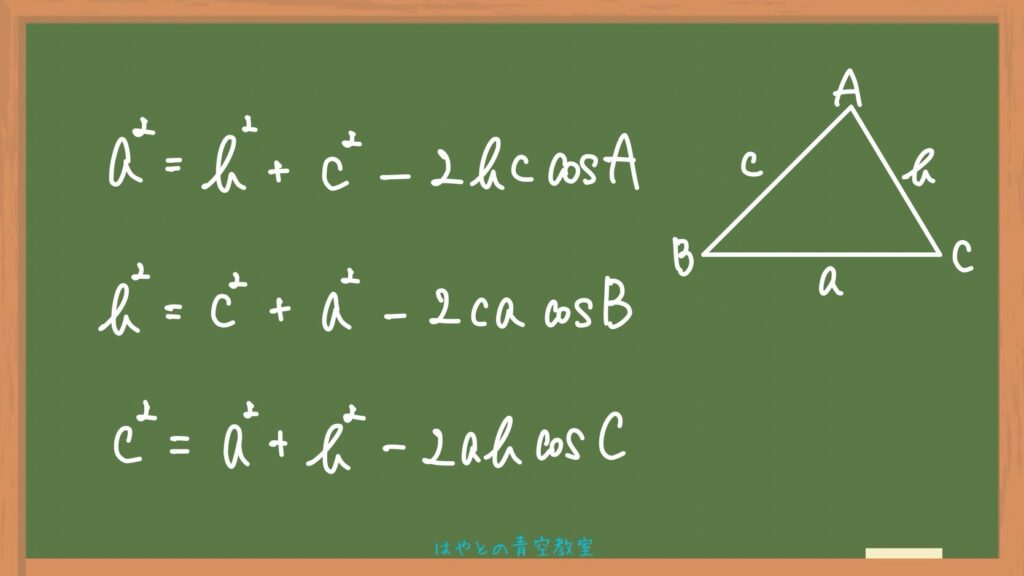
証明
こちらも、Aについて着目した証明を紹介します。
B、Cについても同様にして、定理の式を導くことができます。
三角形の面積
最後にsinを使った三角形の面積の公式です。
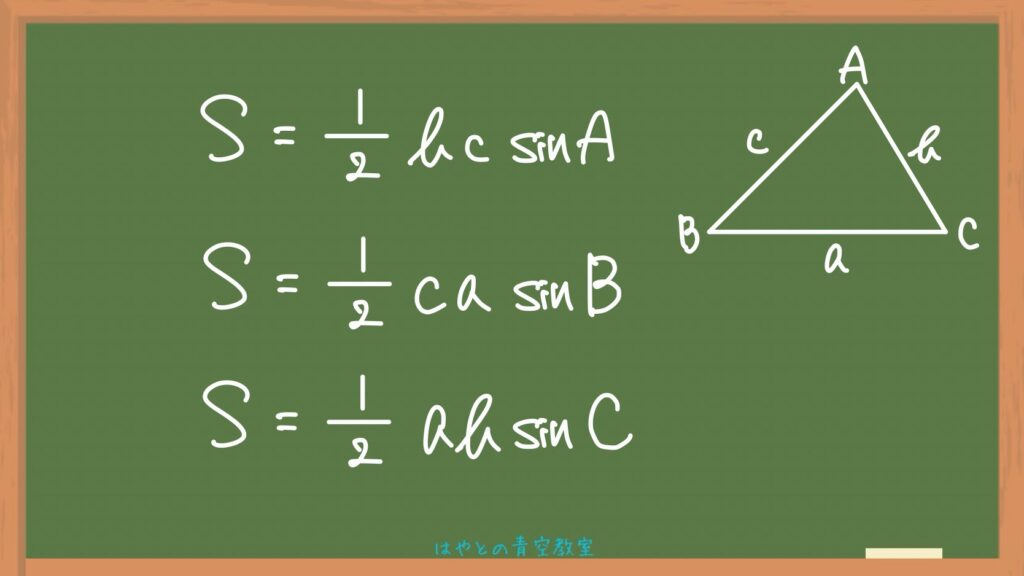
証明
こちらもAについて着目した証明を紹介します。
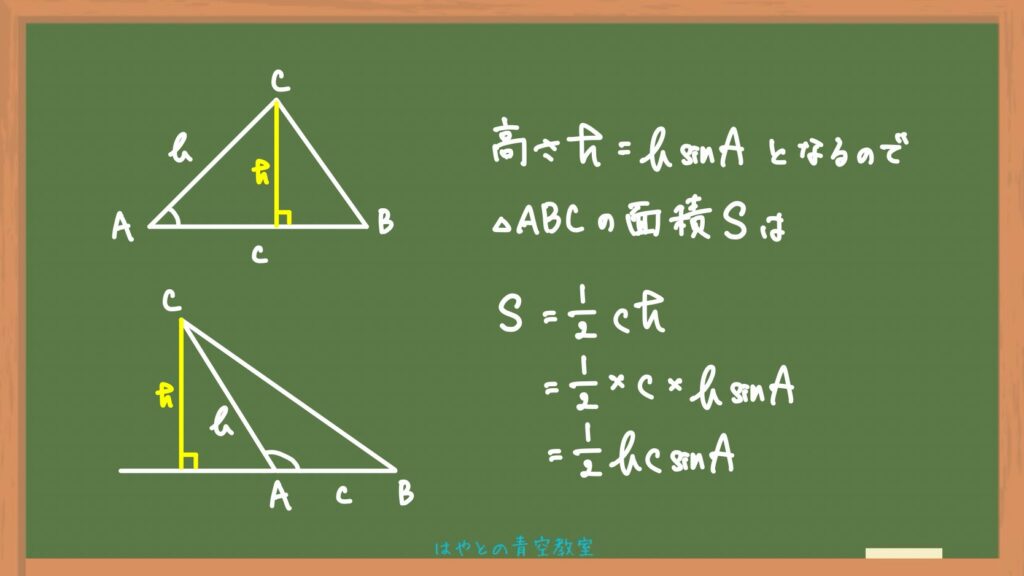
B、Cについても同様にして公式を導くことができます。
使い方
公式では3つ式を紹介し、少し文字が多いようにも見えたかもしれません。
しかし、実際に使うときには2つの辺とその間の角さえわかってればok！
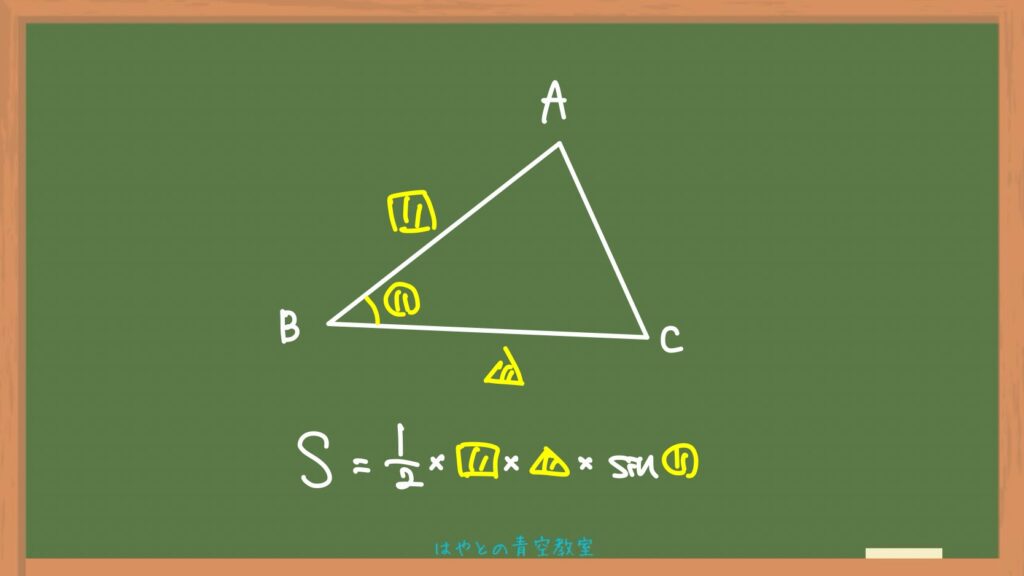
2つの辺と、その間の角のsinから三角形の面積を求めることができるんです。
公式を文字で覚えるより、このように図で覚えちゃいましょう！
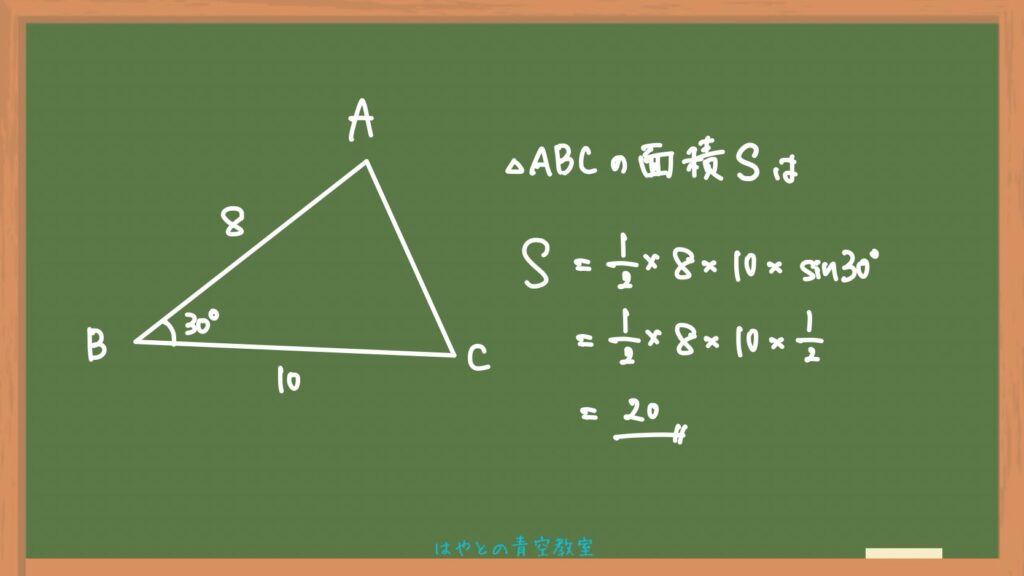
例題
実際に数字を入れた例題を紹介しておきます。
さいごに
この記事では、三角比の定理とその証明について解説しました！
それぞれ、何がわかっていたら使うことができるのかおさえて、上手に問題を解くときに活用してください！
どうせやるなら楽しんで！
はやとの青空教室では、「数学がわかることで毎日の授業や数学の勉強が楽しくなったらいいな」という想いで数学の解説をしています！
確認したい公式が一目で見つかる、高校数学の公式をまとめた記事も公開しています⬇️
合わせて読みたい
【高校数学公式一覧】新課程に対応して現役数学講師が徹底解説！
また、数学の苦手克服、志望校合格にオススメな塾も紹介していますので、こちらもぜひ参考にしてみてください😌
オススメの塾を紹介！
【数強塾の口コミ・評判は？】現役数学講師が徹底分析！
【坪田塾で数学は得意になれるのか？】口コミと特徴から現役数学講師が徹底分析！
【坪田塾オンライン校の口コミ】現役数学講師が徹底分析！
塾選びに迷ったらこちらの記事がオススメです⬇️
合わせて読みたい
【塾選び】自分に合った授業形態の選び方のポイントを解説！
「このサイトが参考になった！」と思ったら是非お友達にも紹介してください！
数学や進路についての質問・相談がありましたら、お気軽に下のコメントから送ってください！お待ちしています！
ABOUT ME
7年目数学講師。中高数学非常勤講師／対面・オンライン家庭教師→公営塾スタッフ（地域おこし協力隊）▶︎数学の解説や塾選び、自身の体験談などについて記事にしています。
