【2次関数の最小値・最大値】下に凸のグラフの場合分けを現役数学講師が解説！
@hayato0121
はやとの青空教室
【上に凸のグラフの最小値・最大値】場合分けのやり方を現役数学講師が解説！
@hayato0121
記事内に商品プロモーションを含む場合があります
こんにちは！はやとです！
今回は2次関数の最小値と最大値の場合分け、上に凸バージョンを解説します！
「場合分けが苦手」
という声をぼく自身多くの生徒から聞いてきましたが、場合分けはパターンをつかめば難しくありません！
定義域に対して軸を動かしながら考えるとシンプルなので、一緒に頑張りましょう！
『はやとの青空教室』では数学の苦手克服にオススメな塾の紹介もしています！
【数強塾の口コミ・評判は？】現役数学講師が徹底分析！
【坪田塾で数学は得意になれるのか？】口コミと特徴から現役数学講師が徹底分析！
【坪田塾オンライン校の口コミ】現役数学講師が徹底分析！
数学講師歴7年のぼくの視点で解説しています！
目次
最小値の場合分け
ではまず、最小値から見ていきましょう！
上に凸のグラフで最小値を考える場合は、定義域内でちょうど半分になるところを基準に、軸を動かして考えます。
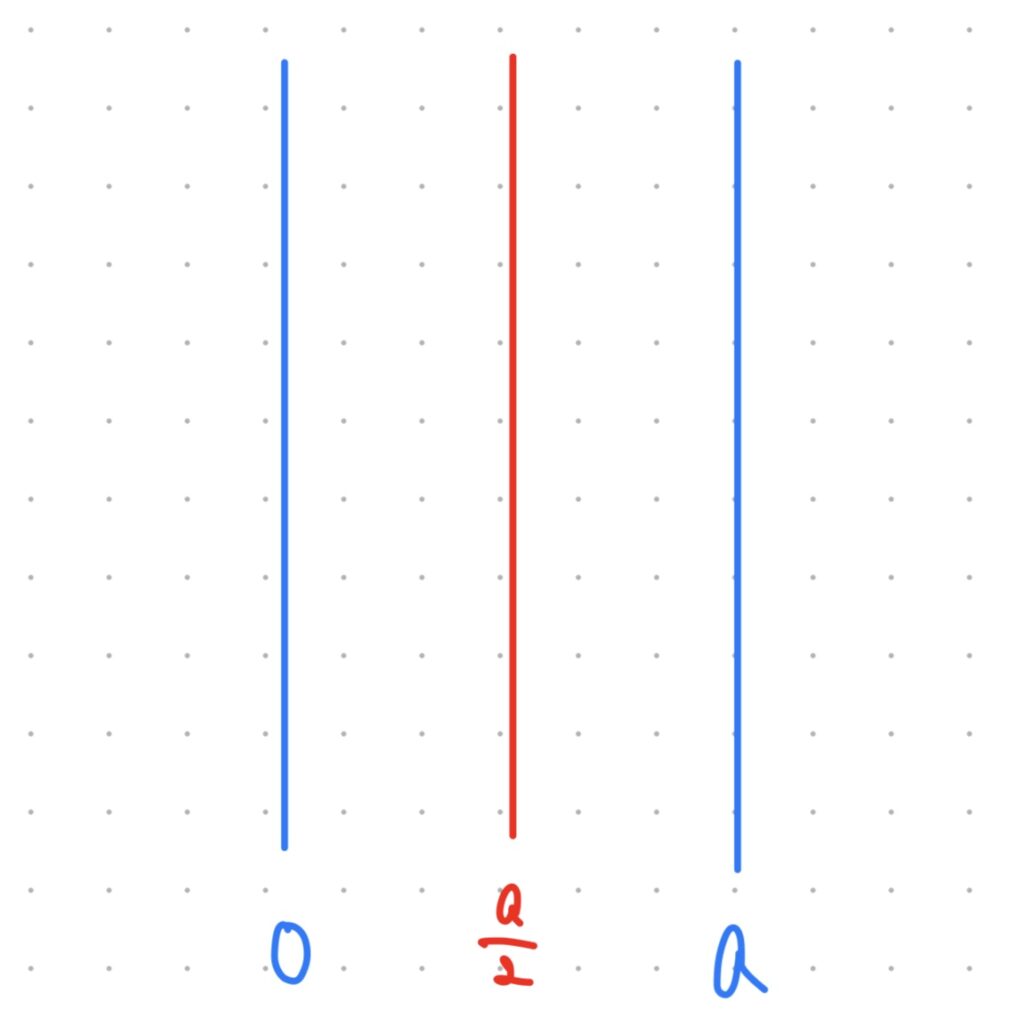
今回、定義域は0以上a以下とするので、ちょうど半分の値はa/2
軸がa/2よりも左側のとき
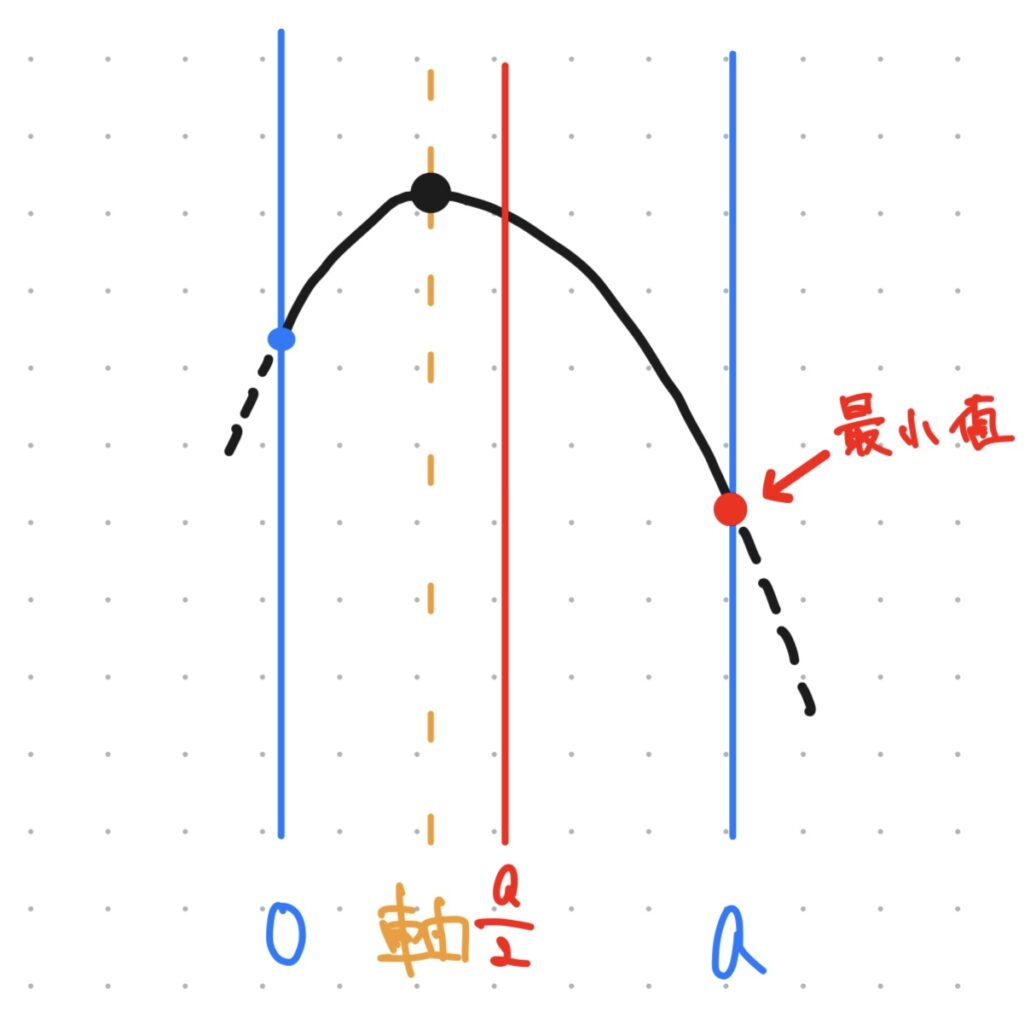
まずは軸がa/2の左側にある場合から。
このとき、グラフは図のようになり、定義域の中ではx=aのとき、最小値をとります。
図では軸が定義域の中にありますが、そのまま左にズラしていって定義域の外側にあったとしても、最小値はx=aでとります。
軸がa/2よりも左側にあるとき、最小値は定義域の右端でとる
軸がa/2よりも右側のとき
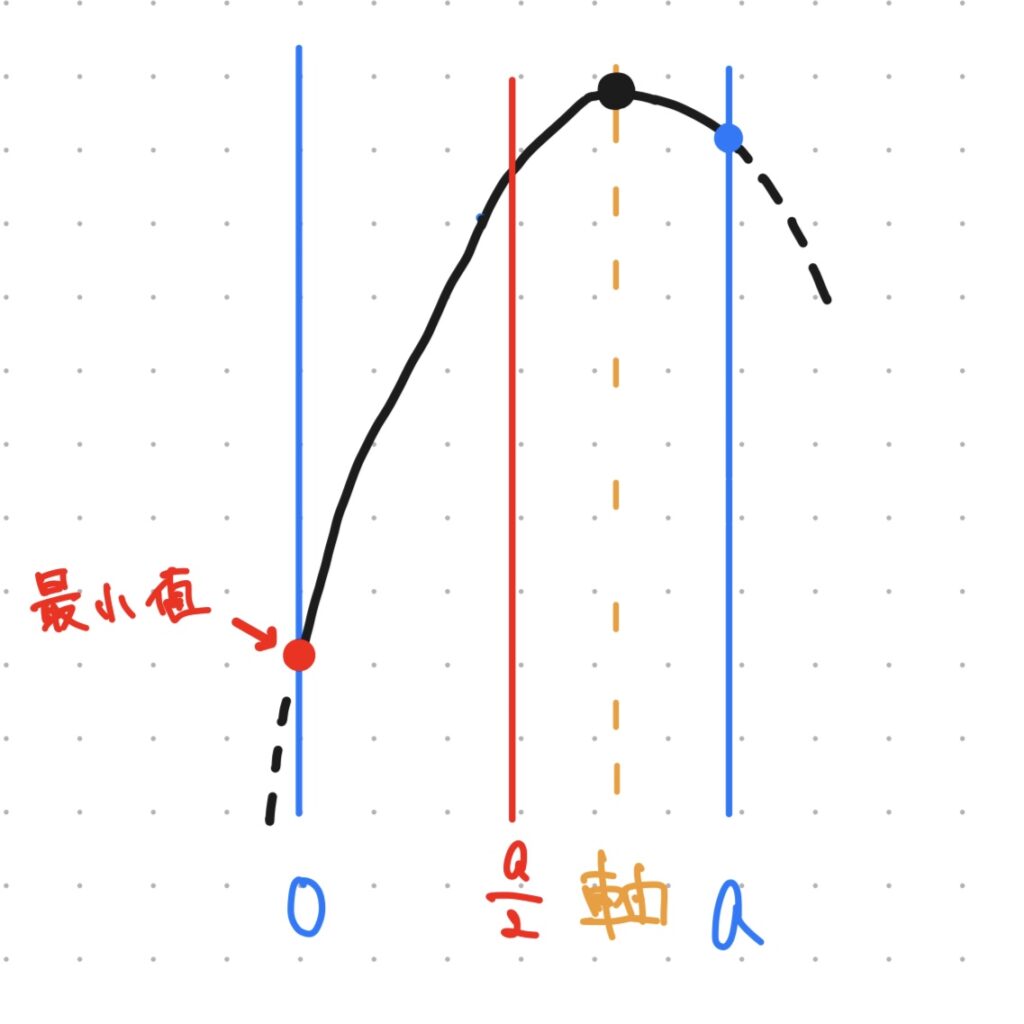
次に、軸を右にずらしていって、a/2よりも右に来た場合について考えてみましょう。
このときのグラフは図のようになり、定義域の中ではx=0のとき、最小値をとります。
図では軸が定義域の中にありますが、そのまま右にズラしていって定義域の外側にあったとしても、最小値はx=0でとります。
軸がa/2よりも右側にあるとき、最小値は定義域の左端でとる
軸がちょうどa/2のとき
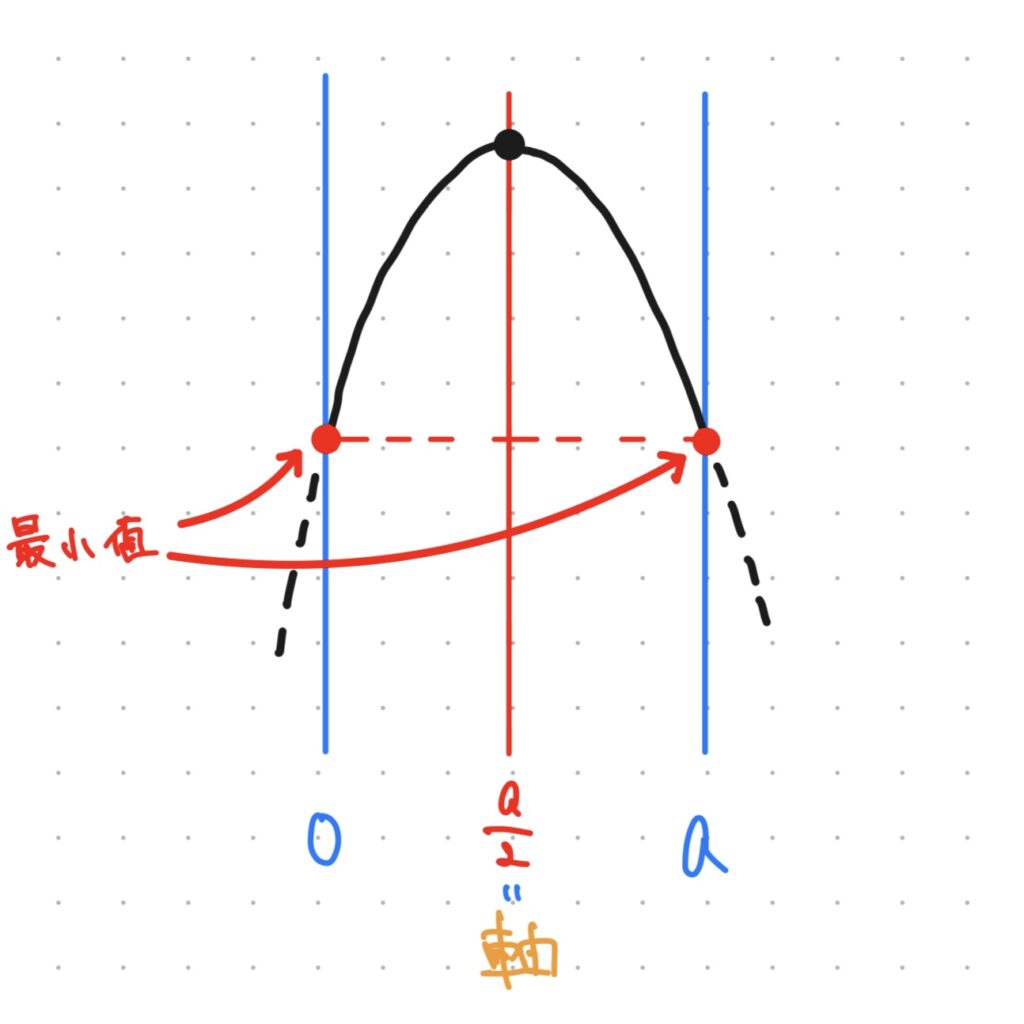
最後に、軸とa/2が重なる場合。
このとき、グラフは図のようになり、x=0のときとx=aの時の値は一致して、どちらも最小値ということになります。
軸がちょうどa/2のとき、最小値は定義域の両端でとる
最小値のまとめ
上に凸なグラフ/最小値を考える場合分け
(i) 軸が定義域の半分よりも左側
最小値は定義域の右端で取る
(ii) 軸が定義域の半分よりも右側
最小値は定義域の左端で取る
(iii) 軸が定義域のちょうど半分
最小値は定義域の両端で取る
最大値の場合分け
次に、最大値について考えていきましょう！
最大値を考える場合は、定義域の中か、外か、という視点で見ていきます。
軸が定義域よりも左側のとき
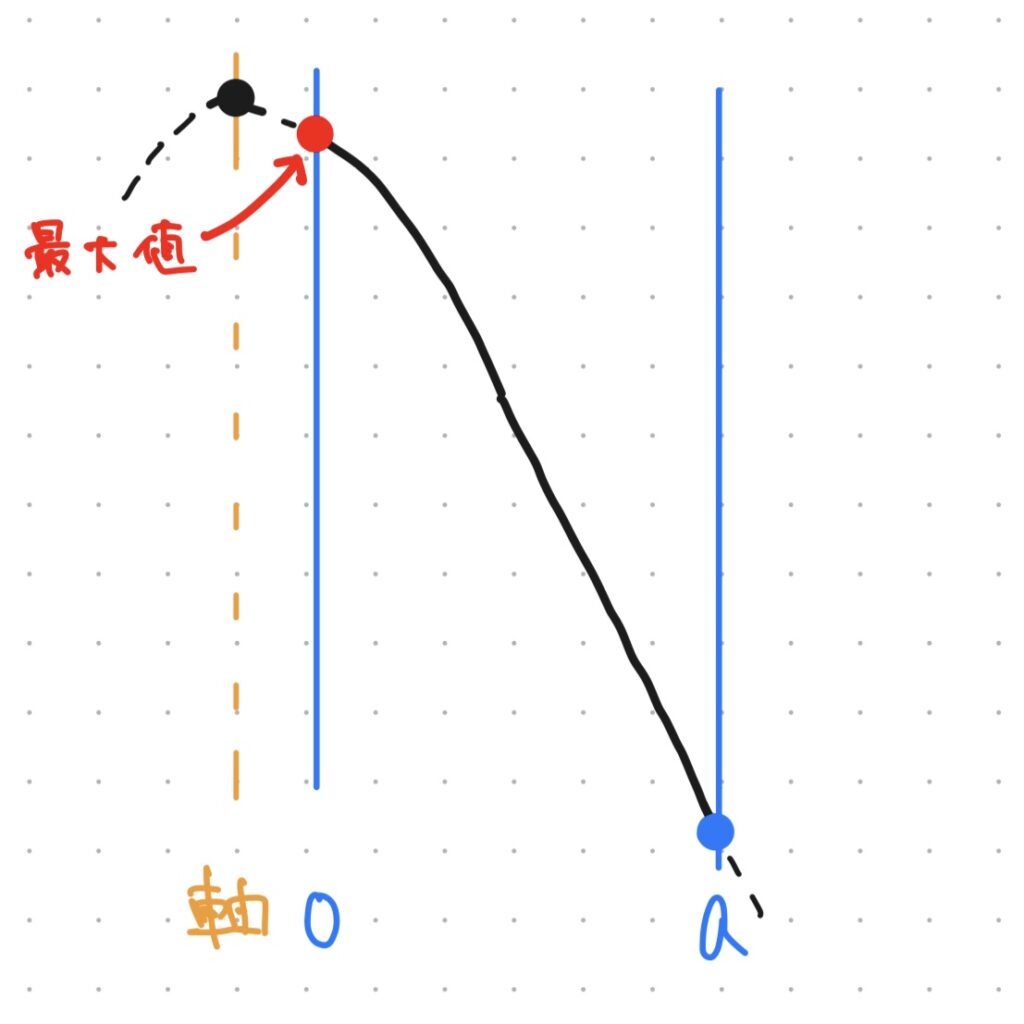
まずは軸が定義域よりも左側にある場合から。
このときのグラフは図のようになり、定義域の中ではx=0のとき、最大値をとります。
軸が定義域よりも左側にあるとき、最大値は定義域の左端で取る
軸が定義域の中のとき
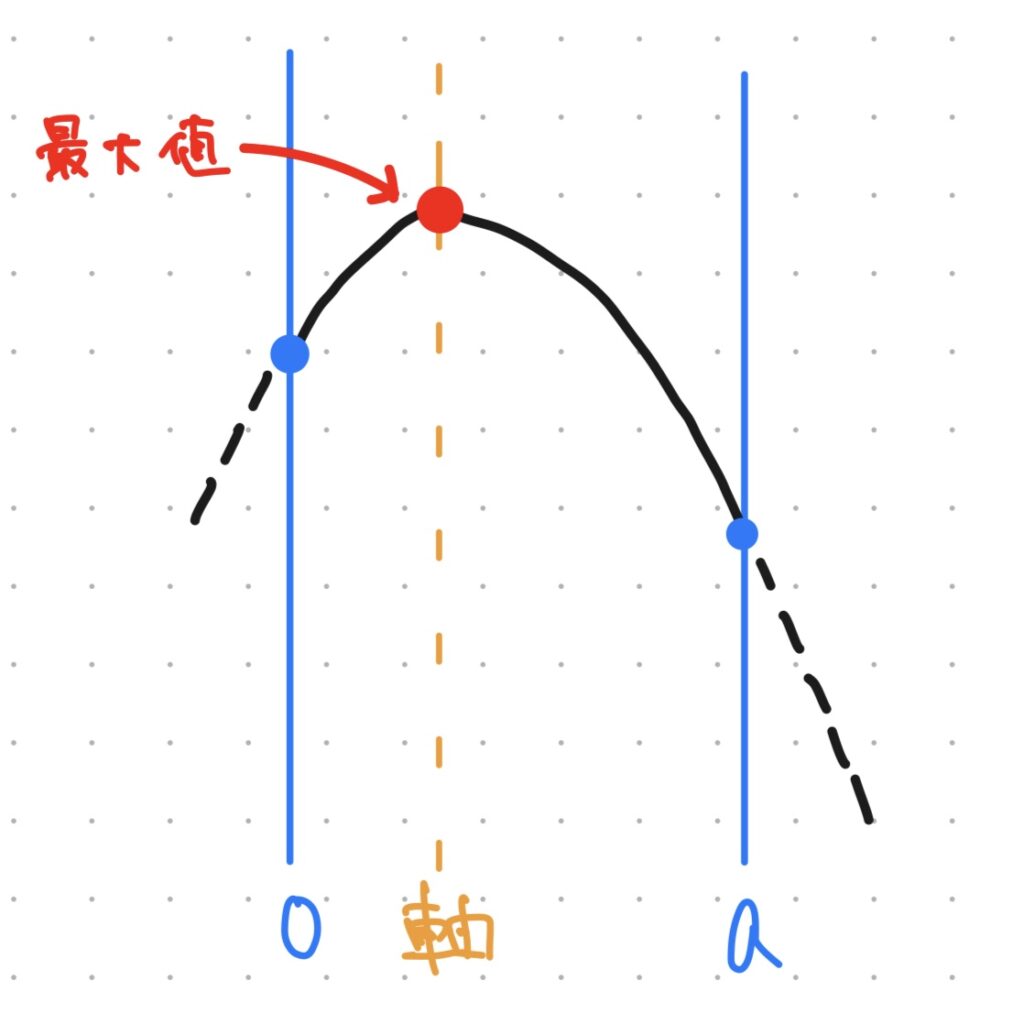
次に、軸が定義域の中にある場合。
このときのグラフは図のようになり、頂点のy座標が最大値となります。
軸が定義域の中にあるとき、最大値は頂点のy座標
軸が定義域よりも右側のとき
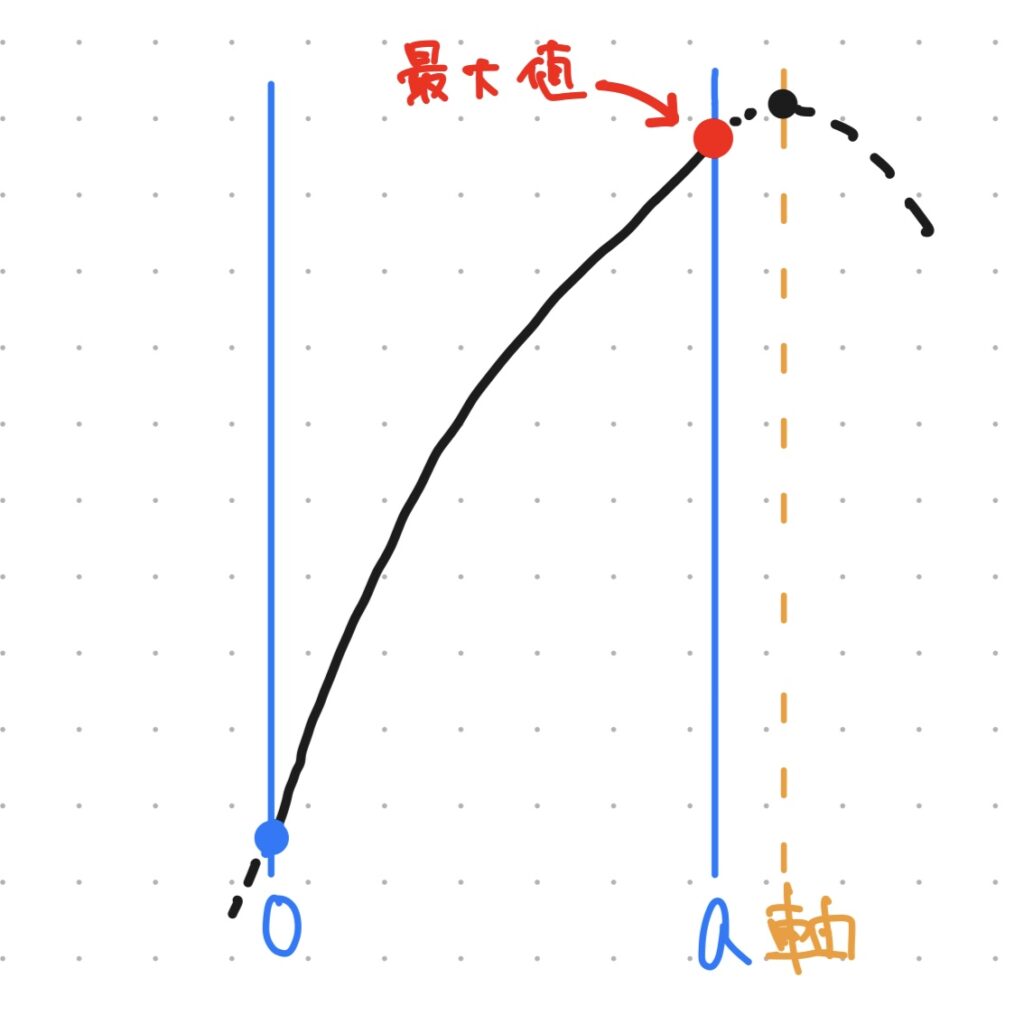
さいごに、軸が定義域よりも右側にある場合。
このときのグラフは図のようになり、定義域の中ではx=aのとき、最大値をとります。
軸が定義域よりも右側にあるとき、最大値は定義域の右端でとる
最大値のまとめ
上に凸なグラフ/最大値を考える場合分け
(i) 軸が定義域よりも左側
最大値は定義域の左端で取る
(ii) 軸が定義域の中
最大値は頂点のy座標
(iii) 軸が定義域よりも右側
最大値は定義域の右端で取る
さいごに
今回は2次関数のグラフの最小値最大値について、場合分けのやり方を解説しました。
最小値と最大値、それぞれ3つずつの場合に分けると簡単に考えることができます！
暗記するのではなく、軸を動かすことでいつ最小値・最大値が変化するのか見ることができますので、自分でできるようになるまで練習してみてください😁
下に凸バージョンはこちらの記事で解説しています⬇️
合わせて読みたい
【2次関数の最小値・最大値】下に凸のグラフの場合分けを現役数学講師が解説！
どうせやるなら楽しんで！
はやとの青空教室では、「数学がわかることで毎日の授業や数学の勉強が楽しくなったらいいな」という想いで数学の解説をしています！
確認したい公式が一目で見つかる、高校数学の公式をまとめた記事も公開しています⬇️
合わせて読みたい
【高校数学公式一覧】新課程に対応して現役数学講師が徹底解説！
数学の苦手克服、志望校合格にオススメな塾も紹介していますので、こちらもぜひ参考にしてみてください😌
オススメの塾を紹介！
【数強塾の口コミ・評判は？】現役数学講師が徹底分析！
【坪田塾で数学は得意になれるのか？】口コミと特徴から現役数学講師が徹底分析！
【坪田塾オンライン校の口コミ】現役数学講師が徹底分析！
塾選びに迷ったらこちらの記事がオススメです⬇️
合わせて読みたい
【塾選び】自分に合った授業形態の選び方のポイントを解説！
「このサイトが参考になった！」と思ったら是非お友達にも紹介してください！
数学や進路についての質問・相談がありましたら、お気軽に下のコメントから送ってください！お待ちしています！
ABOUT ME
7年目数学講師。中高数学非常勤講師／対面・オンライン家庭教師→公営塾スタッフ（地域おこし協力隊）▶︎数学の解説や塾選び、自身の体験談などについて記事にしています。
最小値を考えるとき頂点が定義域の外にあるときを考えなくて良い理由がわかりません
教えて欲しいです
ご質問ありがとうございます！！
いただいたご質問について、下記で説明しますね！
まず、「軸がa/2よりも左側のとき」
記事の中の図では定義域の中に軸がある形で説明をしていますが、「軸がa/2よりも左側」という言葉に【定義域の外の左側】も含んでいるんです。
試しにオレンジで書いた軸をさらに左側にずらして、定義域の外側で考えてみたときに最小値はどこで取るかというと、x=aのときで定義域の中に軸があるときと変わりません。
だから、「a/2よりも左側」というだけで定義域の内側も外側のことも考えていて、どちらもx=aのときに最小値を取ることになります。
もう1つの「軸がa/2よりも右側のとき」
こちらも同様に、この一言で定義域の外の右側も含んでいるんです。
この時、定義域の内側でも外側でも軸がa/2よりも右側にあれば最小値はx=0でとります。
記事内の図では定義域の中で説明していましたが、実は定義域の外に軸があるときのことも考えていたんです。
わかりづらい点がありましたら、またご質問ください。